VENUS, LA PLANETE MYSTERIEUSE

LA RARETE DES TRANSITS DE VENUS :

UNE BELLE PRISE DE TETE !

Si vous observez attentivement les dates des transits de Vénus devant le Soleil, une périodicité complexe mais indiscutable apparaît

Ces deux conditions ne sont que très rarement remplies simultanément, ce qui s'explique par les caractéristiques des mouvements orbitaux de Vénus et de la Terre. Notre planète boucle son orbite autour du Soleil en 365 jours 1/4, alors qu'il ne faut que 225 jours à Vénus pour accomplir le même mouvement de révolution autour du Soleil. Il est facile de calculer que la Terre, Vénus et le Soleil ne peuvent en ce cas être alignés que tous les "n" jours selon l'équation 1/n = 1/225 - 1/365, ce qui donne une valeur de n = 584 jours. Pourtant, il n'y a pas de transit de Vénus tous les 584 jours, comme vous pouvez le constater sur le tableau ci-dessus. La cause en est l'inclinaison respective des plans orbitaux de Vénus et de la Terre, comme vous le montre le schéma ci-dessous.

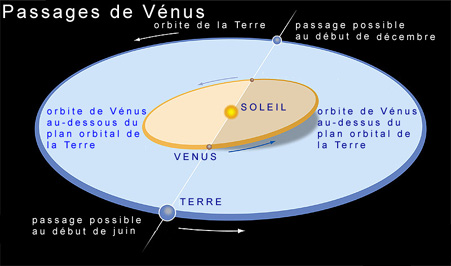
La conséquence pratique de cette inclinaison est que si Vénus et la Terre se retrouvent effectivement alignées tous les 584 jours (les astronomes appellent cette période la révolution synodique), Vénus se trouve par contre, pour un observateur terrestre, en général un peu au-dessus ou bien un peu au-dessous du Soleil.

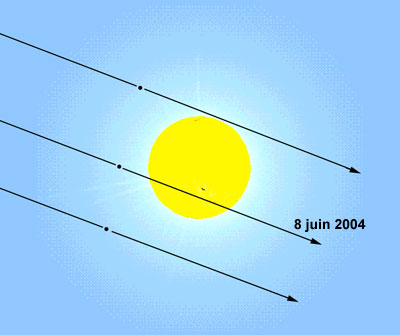
Le 8 juin 2004, l'alignement Soleil-Vénus-Terre aura lieu au moment précis où Vénus se trouvera sur la ligne des noeuds des plans orbitaux de la Terre et de Vénus. Le retour de Vénus sur ces noeuds s'appelle la révolution draconitique. Il ne peut donc y avoir de transit que lorsque la révolution draconitique et la révolution synodique coïncident : le retour des transits doit donc impérativement être une période qui soit un multiple de chacune de ces deux révolutions. Et c'est là que les matheux vont tiquer : comment peut-on donc identifier le rapport des durées des révolutions, qui est un nombre réel, et le rapport du nombre de révolutions, qui est une fraction rationnelle ? Enfer et damnation, c'est impossible ! Heureusement, la Nature permet quelques petits arrangements avec la rigueur mathématique : le disque apparent du Soleil dans le ciel est suffisamment grand, par rapport à celui de Vénus, pour ménager une bonne marge de tolérance et permettre à la planète de passer devant le disque solaire sans forcément passer exactement par le centre de ce dernier.

Si l'on tient compte de cette approximation, on peut dégager "grosso modo" une tendance à voir les transits de Vénus revenir selon un cycle de 8 ans, 121.5 ans, 8 ans, 105.5 ans et ainsi de suite pendant 2500 ans. Au terme de ces 2500 ans, un nouveau cycle commencera pendant lequel le transit se reproduira tous les 121.5 ans seulement, pendant 1000 ans. Une fois ce cycle de 1000 ans terminé, Vénus reprendra le cycle de 2500 ans. Fastoche....................................

Si cette page vous a donné envie d'en savoir plus sur l'observation de Vénus, n'hésitez pas à consulter les liens ci-dessous :
Allez, bonne balade dans les nuages de la planète de la déesse de l'amour !