|
A première vue, faire calculer de façon expérimentale
la distance Terre-Soleil à des enfants de CM2 pouvait
apparaître comme une mission impossible. Mais grâce
aux astucieux conseils du site internet "La
Main à la Pâte", c'est devenu un jeu
auquel les enfants de l'école primaire de Toussaint
se sont attelés avec succès, avec l'aide de
la planète Vénus, lorsqu'elle est passée
devant le Soleil ce 8 juin 2004.

Tout au long du mois de mai, les enfants de l'école
ont préparé ce grand rendz-vous en se livrant
à plusieurs petites expériences, partant du
principe que le 8 juin ils allaient pouvoir observer l'ombre
de Vénus se projeter sur le disque du Soleil

Plusieurs éléments peuvent changer le diamètre
apparent de cette ombre chinoise sur le Soleil : la taille
de Vénus, la distance qui la sépare de la Terre,
la distance qui la sépare du Soleil. Les enfants ont
pu tester eux-mêmes ces différents éléments
en remplaçant Vénus par leur doigt et en réalisant
des visées en direction de la fenêtre de leur
classe. Amusez-vous à renouveler cette expérience
: si vous tendez votre doigt à bout de bras, quelle
partie de la fenêtre masque-t'il ? Si vous rapprochez
votre doigt de votre visage, que masque-t'il maintenant ?
En approfondissant leurs expériences, les enfants
ont découvert que la taille de l'ombre de Vénus
sur le Soleil dépendait étroitement de sa distance.
En remplaçant leur doigt par un petit disque de carton
symbolisant Vénus et en observant sa projection sur
le Soleil, un simple bout de ficelle leur a permis de faire
cette découverte : si l'ombre de Vénus sur la
cible représentant le Soleil est égale à
2 fois la taille de Vénus, alors la distance entre
l'observateur et le disque du Soleil est égale à
2 fois la longueur de ficelle qui va de l'observateur à
Vénus

Un peu plus tard, nouvelle expérience, nouvelle découverte
: si l'ombre de Vénus sur le disque solaire est égale
à 3 fois la taille de Vénus, alors la distance
entre l'observateur et le Soleil est égale à
3 fois le bout de ficelle qui va de l'observateur à
Vénus. Il existe donc une RELATION PROPORTIONNELLE
entre la distance Terre-Soleil et le diamètre de l'ombre
de Vénus devant le Soleil.

L'utilisation de petits dessins géométriques
a permis mieux comprendre ce qui se passait .

C'est dessins peuvent se simplifier en se limitant à
représenter des triangles dont les sommets sont formés
par l'observateur terrestre et les diamètres de Vénus
et du cercle de son ombre projetée sur le Soleil.
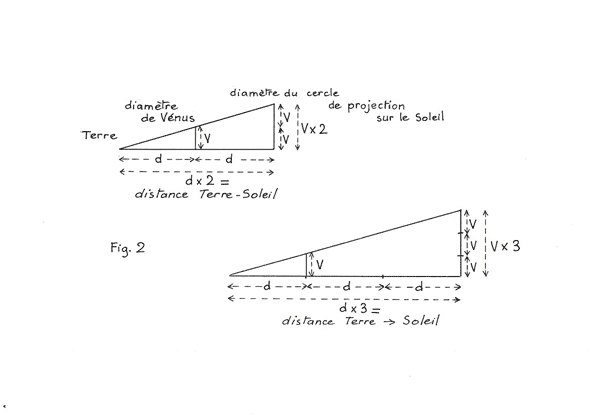
En prenant le triangle schématisant le cas de figure
où l'ombre de Vénus était égale
à 3 fois le diamètre réel de Vénus,
les enfants se sont livrés à plusieurs exercices
de calcul sur des feuilles quadrillées, qui leur ont
permis de faire une nouvelle découverte très
étonnante : si l'ombre est 3 fois plus grande que Vénus,
la distance Terre-Soleil est elle aussi 3 fois plus grande
que la distance Terre-Vénus. Mais ce n'est pas tout
: on retrouve d'autres rapports constants en essayant d'autres
combinaisons, comme le montre le petit dessin ci-dessous.

Ces proportions constantes entre le triangle délimité
par Vénus et la Terre d'une part, et le triangle délimité
par Vénus et le Soleil d'autre part, ont été
découvertes il y a très très longtemps,
par un astronome et philosophe grec : Thalès de Milet,
qui en a tiré le "théorème des triangles
semblables" que vous avez vous-mêmes appris il
y très longtemps, sur les bancs de l'école.
Une idée a alors germé : pourquoi ne pas se
servir de ce théorème le jour du passage de
Vénus devant le Soleil ? En comparant la taille de
l'ombre de Vénus devant le Soleil avec son diamètre
réel, on allait pouvoir découvrir ce fameux
rapport constant, lequel serait alors facilement réutilisable
pour obtenir la distance Terre-Soleil. Dans l'exemple ci-dessus,
le rapport était de 3 : à une ombre de Vénus
3 fois plus grosse que Vénus elle-même correspond
une distance Terre-Soleil 3 fois plus grande que la distance
Terre-Vénus. Ce calcul est la portée de n'importe
quel écolier !
A ce stade de leurs expériences, les enfants se sont
heurtés à plusieurs questions pratiques : comment
mesurer exactement le diamètre du Soleil et celui de
l'ombre de Vénus ? Quelle est la valeur de la distance
Terre-Vénus ? Quel est le diamètre réel
de la planète Vénus ?
Pour réussir les mesures, le club d'astronomie de
Toussaint a fourni aux enfants un Solarscope, petit instrument
permettant de projeter sur un écran, sans risque pour
les yeux, l'image du Soleil et de Vénus.

Au fond du Solarscope ont été placés
deux gabarits : un pour le Soleil, formé de plusieurs
cercles concentriques dessinés par les enfants avec
leurs compas. La règle du jeu consiste alors à
placer l'image du Soleil sur ce gabarit pour voir quel cercle
correspond le mieux à la taille de l'image du Soleil.

Même principe pour mesurer la taille de l'ombre de
Vénus : un petit gabarit représentant plusieurs
cercles de diamètres différents a été
collé juste à côté du gabarit solaire.
Le 8 juin, le travail des enfants a alors consisté
à trouver dans lequel de ces petits cercles l'ombre
de Vénus rentrait le mieux.

Grâce aux gabarits confectionnés par leurs soins,
les enfant sont ainsi parvenus à mesurer, le 8 juin,
la taille de l'image du Soleil projetée par le Solarscope
: 112 mm, ainsi que la taille de l'ombre de Vénus sur
le Soleil : 4 mm.

Ces problèmes pratiques de mesures résolus,
restait la question des données manquantes pour réussir
le calcul de la distance Terre- Soleil : les enfants ignoraient
la taile réelle de Vénus, ainsi que la distance
Terre-Vénus. Pour les aider , 3 indices leur ont été
fournis :
1° indice : le diamètre réel du Soleil
est de 1 400 000 km (les chiffres ont été
arrondis pour faciliter le travail des enfants).
2° indice : le Soleil est 115 fois plus gros que la
planète Vénus.
3° indice : la distance Terre-Vénus est égale
à 30 fois le diamètre du Soleil.

Une petite multiplication toute bête a permis d'employer
le 1° indice pour trouver le 3° : la distance Terre-Vénus
= 1 400 000 x 30 = 42 000 000 km.
Ce même 1° indice a également permis, au
passage, de connaître le diamètre réel
de Vénus : 1 400 000 / 115 = 12 174 km .
Les indices 1 et 2 ont débouché sur une autre
conclusion pratique : le diamètre du Soleil mesuré
le 8 juin dans le Solarscope était de 112 mm. A la
même échelle, le diamètre de Vénus
aurait dû être par conséquent de 112 /
115 = 0,974 mm. Or, grâce à leur gabarit, les
enfant ont trouvé que l'ombre de Vénus était
bien plus grosse, et qu'elle mesurait en fait 4 mm.

En comparant ce diamètre théorique de 0,974
mm et le diamètre réel de l'ombre, de 4 mm,
une simple division a permis de trouver qu'il existait un
rapport de 4 / 0,974 = 4,107 entre eux.
Celà signifiait donc que la taille de l'ombre de Vénus
sur le Soleil était 4,107 fois plus grosse que la taille
réelle de Vénus. A partir de là, le fameux
théorème de Thalès de Milet donne cette
conclusion toute bête : si le rapport entre la taille
de l'ombre de Vénus et son diamètre réel
est de 4,107, alors le rapport entre la distance Terre-Soleil
et la distance Terre-Vénus sera aussi de 4,107. En
clair : la distance Terre-Soleil sera égale à
4,107 fois la distance Terre-Vénus.
Grâce au 3° indice, les enfants savaient que la
distance Terre-Vénus représente 30 fois le diamètre
réel du Soleil, soit une valeur de 42 000 000 km. Par
conséquent, la distance Terre-Soleil = 4,107 x 42 000
000 = 172 494 000 km. Pour simplifier, les enfants ont arrondi
leur résultat à 173 millions de kilomètres.
Ce chiffre n'est pas très éloigné de
la valeur réelle de la distance Terre-Soleil calculée
par les astronomes : 149 600 000 km. L'erreur de 22 894 000
km faite par les élèves de l'école primaire
de Toussaint s'explique facilement par les imprécisions
de leurs mesures, les gabarits étant des outils de
mesure très rudimentaires : une erreur de 1 mm dans
l'estimation du diamètre du Soleil entraîne une
erreur de plus de 1,5 millions de kilomètres dans le
calcul de la distance Terre-Soleil. Et pour la mesure de l'ombre
de Vénus, les choses sont encore bien pires : une petite
erreur d'un malheureux demi-millimètre dans la mesure
entraîne une erreur de près de 22 millions de
kilomètres dans le calcul de la distance Terre-Soleil.
Dans ces conditions, les enfants de l'école de Toussaint
méritent donc de réelles félicitations
: chapeau les astromômes !!!



|