|
Cette méthode est inspirée de celle proposée
par les auteurs de l'excellent livre "Vénus devant
le Soleil", publié par les éditions
Vuibert - Adapt, et qui constitue une véritable
mine de renseignements pour tout astronome amateur désireux
de comprendre le transit de Vénus devant le Soleil.

Cette méthode s'apparente à celle qu'élabora
Edmund Halley, avec quelques simplifications
(ouf !). Le point de départ repose cependant sur le
même raisonnement que celui que fit Edmund Halley en
1716. Selon que l'observateur est placé sur le globe
terrestre en A ou en B, il verra Vénus sur le Soleil
respectivement en A' et en B'.

Schéma 1 : ASCT-astronomie
Le trajet que décrit Vénus sur le Soleil, depuis
son entrée sur le disque solaire jusqu'à sa
sortie, dessine une droite, appelée "corde"
: le schéma ci-dessus montre bien ces deux cordes.
Pour l'observateur A, la corde suivie par Vénus va
de a1 à a2. Pour l'observateur B, la corde va de b1
à b2. Les deux cordes sont séparées par
une distance e.
- Première constatation : si les observateurs A et
B sont trop proches, "e" sera trop faible et les
deux cordes se superposeront sans que l'on puisse distinguer
l'une de l'autre. La méthode Halley implique donc
que les deux équipes d'astronomes soient les plus
éloignées possible, l'une dans l'hémisphère
Nord et l'autre dans l'hémisphère Sud
- Deuxième constatation : observée depuis le lieu
B, Vénus suit une corde plus courte que vue depuis A : le
passage de Vénus devant le Soleil durera donc moins
longtemps pour l'observateur B que pour l'observateur A
Le calcul de la valeur de "e" constitue la première
étape de nos calculs. Il s'agit d'un calcul simple,
qui fait appel au bon vieux théorème de Thalès
sur les triangles semblables : les triangles AVB et A'VB'
sont effectivement des triangles semblables

Schéma 1 : ASCT-astronomie
Si dvs est la distance séparant Vénus du Soleil
et dtv celle qui sépare la Terre de Vénus, on
en conclut, grâce au théorème de Thalès,
que :

La troisième loi de Képler établit qu'il
existe un rapport constant entre les distances des planètes
et leurs vitesse de révolution autour du Soleil. Etablies
en 1629, ces lois étaient donc bien connues de Halley,
en 1716. Il eût l'idée de s'en servir pour exprimer
les distances dst et dsv
Par convention, appelons Tt la période de révolution
de la Terre autour du Soleil et dst la distance qui les sépare,
et faisons-en de même pour Vénus avec Tv pour
la période de révolution et dsv la distance
Vénus-Soleil. La troisième loi de Képler
énonce alors que :

La loi de Képler permet alors à Edmund Halley
de réécrire l'équation de "e"
comme suit :

Les durées de révolution de la Terre et de
Vénus autour du Soleil étaient déjà
bien connues au XVII° siècle : la Terre met environ
365 jours pour boucler son orbite et Vénus 225 jours.
Grâce à ces chiffres, l'équation de "e"
va devenir tout bêtement :

Par exemple, si la distance AB séparant les deux équipes
d'astronomes est de 4000 km, "e" aura une valeur
d'environ 10 500 km
Ce n'est qu'arrivés à ce point que nous allons
simplifier un peu les calculs d'Edmund Halley, en nous aidant
du diamètre du Soleil. Exprimé en radians, le
diamètre apparent du Soleil tel que nous le voyons
dans le ciel est égal à son diamètre
réel, divisé par la distance qui le sépare
de la Terre

Or, le diamètre réel du Soleil est facile à
évaluer grâce au transit de Vénus : reprenez
le schéma 1. S'il était à l'échelle,
comme ce sera le cas sur les photographies que vous effectuerez
le 8 juin prochain, vous pourriez constater que le Soleil
est 133 fois plus large que "e".
|
|
|
|
Les photographies de l'observateur
A |
Les photographies de l'observateur
B |
|
|
|
La superposition des deux photographies
permet de mesurer le rapport diamètre solaire
/ e |
Une simple multiplication vous suffit alors pour démontrer
que le Soleil mesure 133 x e = 1 396 000 km.
Une mesure du diamètre apparent du Soleil donne 32
minutes d'arc, soit un peu moins de 1/100 de radian. Il ne
vous reste plus qu'à reprendre l'équation précédente
et vous aurez alors le résultat de la distance Terre-Soleil
: dst = 150 000 000 km approximativement. Sachant que la valeur
réelle est de 149 600 000 km, appréciez la performance...
Et toc...
D'autres méthodes sont possibles :
Le comité
de liaison enseignants-astronomes propose une méthode
adaptée aux astrophotographes : il s'agit de superposer,
comme précédemment, deux photos prises au même
instant et de mesurer le chevauchement de l'image de Vénus.
|
|
|
|
|
Photo prise à Dijon |
Photo prise à La Réunion |
Superposition des photos |
Simulation d'images réalisées simultanément
le 8 juin 2004 à 10 H TU
Si vous avez l'intention de calculer la distance Terre-Soleil
par une méthode faisant appel à la photographie,
qu'elle soit argentique, numérique ou bien avec une
webcam, nous vous recommandons de prendre connaissance du
remarquable protocole élaboré
par le CLEA. Et si vous êtes débutants en
astrophotographie, consultez impérativement notre dossier
sur la photographie du Soleil et tout particulièrement
le chapître relatif à la protection de vos yeux
L'institut
de la Mécanique Céleste et de Calcul des Ephémérides
propose de reproduire à l'identique le calcul de la
distance Terre-Soleil très exactement comme au XVIII°
siècle, grâce au chronométrage précis
des différents contacts de Vénus avec le disque
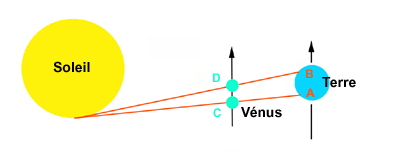
solaire. Le schéma ci-dessous, qui représente
Vénus et la Terre sur leurs orbites autour du Soleil,
illustre cette technique : l'observateur A voit l'entrée
de Vénus sur le disque solaire en C, avant l'observateur
B qui doit attendre que Vénus soit arrivée en
D
Enfin le site européen
Futura-Sciences coordonne tout un programme de mesures
de la distance Terre-Soleil en faisant appel aux deux méthodes
ci-dessus : photographie de la corde de Vénus sur le
Soleil et chronométrage des différents contacts.
N'hésitez pas à vous inscrire afin de participer
à l'une et/ou l'autre de ces grandes opérations
internationales : plus nous serons de fous... |
















