1°) La fabuleuse expérience d’Eratosthène :
Des voyageurs avaient rapporté à Eratosthène que le jour de l’été, à l’instant de midi, le Soleil était tellement haut dans le ciel de Syène (aujourd’hui appelée Assouan) que le puits de Syène en était illuminé jusqu’au fond et qu’un gnomon planté verticalement dans le sol ne portait plus aucune ombre.
Or le même jour, devant la grande bibliothèque d’Alexandrie dont il était le directeur depuis 235 avant JC, Eratosthène constata que le même jour, à la même heure, l’obélisque avait une ombre.

Après une longue réflexion, Eratosthène compris qu’il n’y avait qu’une seule et unique explication : la Terre est ronde et, du fait de la courbure du sol, l’angle que font les rayons du Soleil avec le sol n’est pas le même à Alexandrie et à Syène. A Syène, à midi le jour de l’été, le Soleil est exactement à la verticale, alors qu’à Alexandrie, il est un peu moins haut dans le ciel.
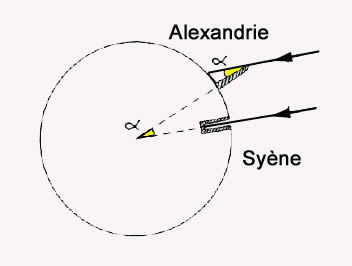
Eratosthène décida de mesurer cet angle, qu’il appela l’angle alpha (en grec, on écrit : α), simultanément à Alexandrie et à Syène, le jour de l’été, à midi précises, au moyen de deux gnomons identiques plantés verticalement dans le sol
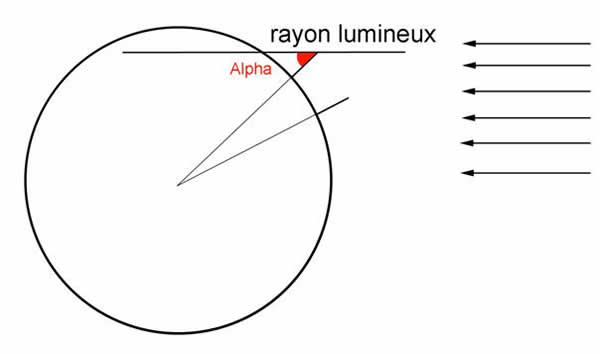
En dessinant sur un papier millimétré (ou bien un papier quadrillé) notre gnomon ainsi que la longueur de son ombre sur le sol, nous avons pu, nous aussi, mesurer facilement avec un rapporteur la valeur de cet angle α
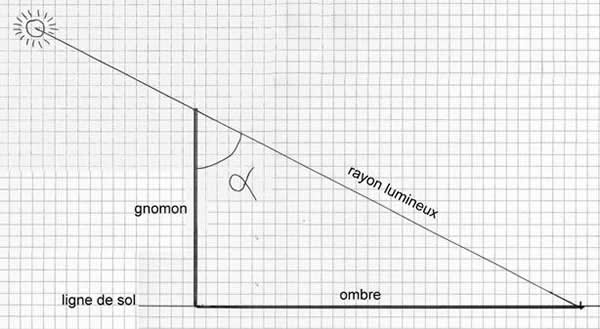
A Syène, le Soleil est à la verticale, ce qui donne un angle α de 0°. Et à Alexandrie, Eratosthène trouva un angle alpha de 7°. Entre Alexandrie et Syène, la différence entre les deux angles alpha est donc de 7 – 0 = 7°
Nous avons tracé puis découpé dans du bristol un petit secteur angulaire de 7°.
Nous avons ensuite dessiné un cercle représentant la Terre.
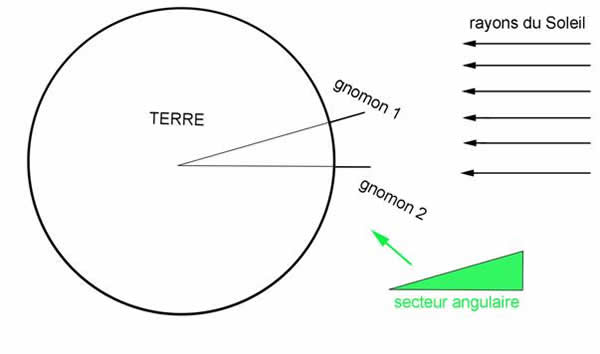
Nous avons alors placé le puits de Syène sur le cercle représentant la Terre, bien à la verticale des rayons solaires.
Puis nous avons fait glisser notre secteur angulaire de bristol sur le cercle de la Terre de telle sorte que le bord représentant les rayons solaires soit bien parallèle à ces derniers, pendant que le bord du secteur représentant le gnomon soit bien vertical et passe donc bien par le centre de la Terre. Le schéma ci-dessous montre comment réaliser cette expérience.
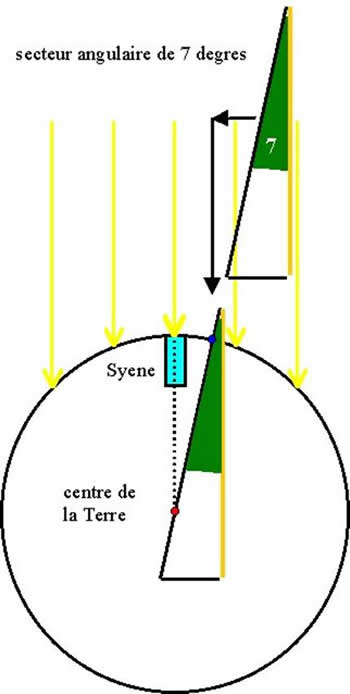
Nous avons découvert qu’il n’y a qu’un seul et unique endroit situé à la surface de la Terre pour lequel les rayons solaires fassent un angle de 7° avec le gnomon planté verticalement : c’est donc à cet endroit-là que se trouvait précisément Alexandrie et son obélisque.
Nous avons alors mesuré sur notre cercle, avec un petit bout de ficelle, la longueur du segment de circonférence qui séparait le gnomon de Syène et celui d’Alexandrie : 8 mm.
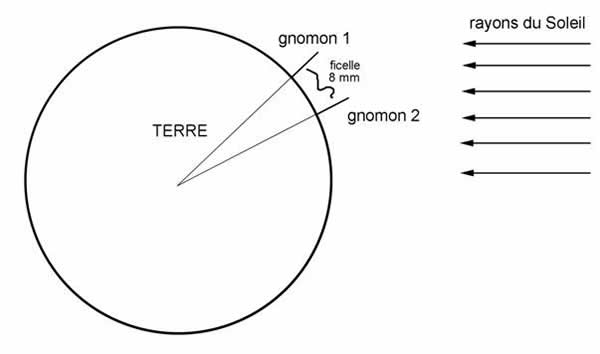
Le raisonnement d’Eratosthène a été le suivant : « si mon dessin reproduit fidèlement ce qui se passe à la surface du globe terrestre, alors les résultats que je vais trouver sur ce dessin pourront être également appliqués à l’ensemble de la Terre » Et il s’est alors posé cette question : « le petit segment de circonférence séparant les gnomons d’Alexandrie et de Syène, et que je viens de mesurer avec ma ficelle, quelle fraction de l’ensemble du cercle représente-il ? »
On peut poser cette question de plusieurs autres façons, en se demandant par exemple : combien de bouts de ficelle faudrait-il pour faire le tour du cercle représentant la Terre ? Ou encore en se demandant : combien de fois y a-t’il de fois le segment Syène-Alexandrie dans la circonférence de la Terre ? Toutes ces questions sont équivalentes. Pour y répondre correctement, il faut faire un calcul de fraction.
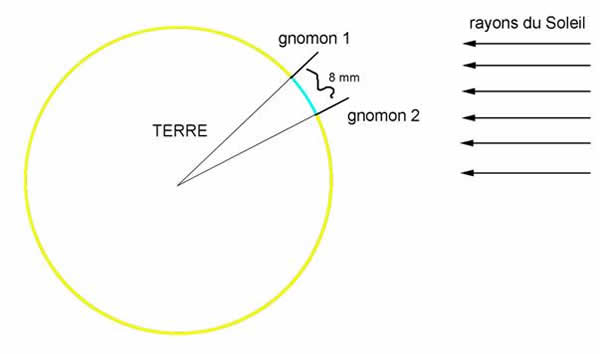
Le calcul de cette fraction est facile à faire : pour savoir combien de fois il y a un petit truc dans un gros machin, il faut diviser le gros machin par le petit truc .
C’est ce que nous avons fait avec le dessin d’Eratosthène : le petit truc, nous l’avons déjà mesuré avec notre bout de ficelle : il fait 0,8 cm sur le schéma.
Il nous manque le gros machin, c'est-à-dire la circonférence de notre cercle. Pour le trouver, Madame Gilles, notre institutrice nous a donné la formule magique inventée par les grecs de l’Antiquité : la circonférence d’un cercle se calcule en multipliant son diamètre D par le chiffre grec π (= Pi), qui vaut 3,14.
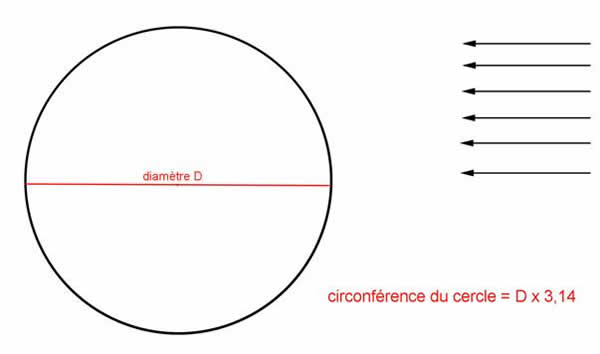
Sur notre dessin, le diamètre du cercle représentant la Terre était de 12,7 cm. La formule magique précédente nous a permis de calculer que la circonférence du cercle était d’environ 39,88 cm.
Voilà, maintenant nous connaissons la valeur de notre gros machin ( 39,88 cm) et la valeur de notre petit truc ( 0,8 cm). Nous pouvons maintenant réussir notre calcul de la fraction et savoir combien de fois il y a 0,8 cm dans la circonférence de notre cercle.
39,88 / 0,8 = 49,85 ce qui donne 50 en arrondissant.
Cela signifie que nos 8 petits millimètres, représentent à peu près la 50 ème partie de l’ensemble du cercle entier : on bouclerait la circonférence entière de ce cercle en mettant bout à bout 50 fois notre ficelle de 8 mm.
Or, la distance réelle entre Alexandrie et Syène était déjà connue à l’époque d’Eratosthène : 5000 stades, ce qui correspond à 800 km. Le raisonnement d’Eratosthène fut alors le suivant : « si, sur mon dessin, les 8 mm séparant Syène d’Alexandrie représentent la 50ème partie de la circonférence du cercle représentant la Terre , alors les 800 km qui séparent réellement ces deux villes représentent eux aussi la 50ème partie de la circonférence réelle de la Terre. Par conséquent, la Terre mesure : 800 km x 50 = 40 000 km. »
Admirez le génie d’Eratosthène : la circonférence réelle de la Terre, mesurée entre le pôle nord et le pôle sud, est de 40 007 km !!!!

2°) Nous refaisons à Toussaint et à Vayres ce qu’Eratosthène a fait à Alexandrie et à Syène :
Ce mois de mai, nous avons essayé de refaire la même chose entre Toussaint et Vayres que ce qu’avait fait Eratosthène avec les villes d’Alexandrie et de Syène, mais nos résultats ont été moins réussis …………………..
A 14 heures, heure d’été (= 12 h en heure solaire), la longueur de l’ombre des gnomons de 10 cm était de 5,6 cm à Vayres et de 4,6 cm à Toussaint.
Comme les semaines précédentes, nous avons recopié ces résultats sur du papier millimétré afin de calculer l’angle alpha, qui s’est avéré être de 25° à Vayres et de 30° à Toussaint. Aujourd’hui, par conséquent, il y avait une différence 30 -25 = 5° entre nos deux villages.
Sur le cercle représentant la Terre, nous avons placé Vayres tout en haut, bien à la verticale des lignes représentant les rayons solaires puis nous avons découpé un secteur angulaire de 5° dans du bristol et l’avons placé sur notre cercle terrestre pour trouver où Toussaint se trouvait par rapport à Vayres.
Là où les choses se sont gâtées, c’est lorsque nous avons constaté que nos cercles n’étaient pas bien ronds et que les diamètres variaient de plus de 10 mm selon l’endroit où on le mesurait. Apparemment, l’imprimante avait fait n’importe quoi… Résultat des courses : toutes nos mesures ont été faussées. Pour certains d’entre nous, la distance entre Vayres et Toussaint était matérialisée sur notre dessin par un petit segment de 5 mm, pour d’autres par un segment de 6 mm et pour d’autres enfin par un segment de 7 mm… Tout ceci a changé bien des choses dans nos calculs de fraction !!!
Notamment, ces quelques petits millimètres de rien du tout représentaient dans le premier cas la 96ème partie de la totalité de la circonférence du cercle, la 80 ème partie dans le deuxième cas de figure et pour ceux d’entre nous qui avaient mesuré 7 mm, la 68 ème partie. Bref, c’était le délire le plus total. De plus, nous nous sommes trompés dans la distance séparant Toussaint de Vayres : nous avons choisi 732 km alors qu’en réalité, il n’y en a que 538……..
Et quand nous avons refait les calculs d’Eratosthène en prenant tous ces mauvais chiffres, nous avons forcément trouvé des résultats complètement farfelus :
Avec une distance Toussaint-Vayres de 732 km et un segment la représentant sur notre dessin de 5 mm, nous avons trouvé une circonférence terrestre de 732 x 96 = 70 272 km !
Celles et ceux d’entre nous qui ont mesuré à 6 mm le segment Toussaint-Vayres, la circonférence terrestre calculée est devenue 58 560 km !!
Et pour celles qui avaient trouvé un segment de 7 mm, la circonférence de la Terre est devenue 49 776 km !!!

La Terre calculée par les élèves de Toussaint le 24 mai 2007...
Bref, nous avons eu tout faux et si Eratosthène avait été là, il nous aurait sans doute tous punis…
Nous essaierons de faire mieux la prochaine fois, c’est promis ! Déjà, en prenant la bonne distance Vayres-Toussaint, c'est-à-dire 538 km, et la mesure de 6 mm du segment représentant sur notre dessin la distance entre nos deux villages, le calcul de la circonférence de la Terre nous a donné un résultat de 43 040 km, ce qui est déjà beaucoup plus proche de la réalité ( 40 007 km) … |