1. L’écho radio et laser :
Pour mesurer la distance de la Terre aux satellites, y compris
notre satellite naturel, la Lune, on peut utiliser la technique
de l'écho radar, ainsi que du faisceau laser : connaissant
la vitesse à laquelle chemine les ondes radio ou bien la
lumière du laser, il suffit pour mesurer la distance nous
séparant du satellite, de calculer le temps mis par l'onde
pour aller jusqu'au satellite et en revenir.
L'une des missions Apollo a d'ailleurs laissé sur la Lune
un réflecteur laser qui mesure en permanence la distance
Terre-Lune avec une précision de quelques centimètres.
Mais cette méthode n'est utilisable que dans la proche banlieue
de la Terre.
2. La méthode des parallaxes :
Pour les étoiles les plus proches de la Terre, les astronomes
emploient la méthode des parallaxes
Dans son grand tour annuel autour du Soleil, la Terre nous emporte,
modifiant légèrement notre angle de vue du ciel.
En particulier, les étoiles les plus proches de la Terre
ne semblent pas au même endroit du ciel si on les regarde
à 6 mois de différence. Et si on observe leur mouvement
durant 12 mois, on constate qu'elles accomplissent un petit cercle
dans le ciel, sur la toile de fond formée par les champs
d'étoiles plus lointaines ainsi que le montre le petit schéma
ci-dessous.
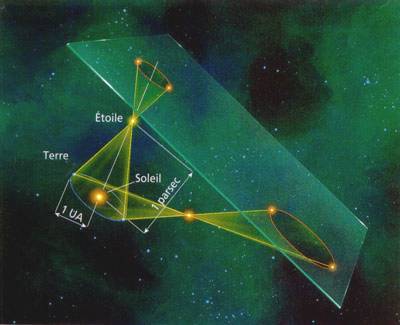
La mesure du déplacement apparent de l'étoile, appelée
parallaxe, est mesurable. Le schéma ci-dessus vous permet
de constater que plus une étoile est proche de nous et plus
l'angle de sa parallaxe est important. A l'inverse, plus une étoile
est éloignée et plus sa parallaxe est faible, difficilement
mesurable
Les astronomes connaissent bien la distance Terre-Soleil (= 1 Unité
Astronomique = 149 597 870 km) : ils peuvent alors calculer sans
problème la distance Terre-étoile, grâce au
théorème de Pythagore ... encore lui !
Au passage, rappelons que c'est cette méthode qui a permis
de définir l'une des unités de mesure employées
en astronomie : le Parsec. Le Parsec est la distance depuis laquelle
le rayon de l'orbite terrestre est vu sous un angle d'une seconde
d'arc
C'est cette méthode qu'a employé de 1989 à
1993 le satellite Hipparcos pour mesurer la distance des étoiles
les plus proches de la Terre.

Le satellite Hipparcos
Travail colossal que celui du satellite Hipparcos : des centaines
de milliers de parallaxes ont été mesurées
par ce satellite, à raison de 115 mesures pour chaque étoile.
Débarrassé des turbulences de l'atmosphère
terrestre, Hipparcos a pu mesurer l'angle de parallaxe de ces étoiles
avec une précision inégalée jusqu'à
présent : 118 218 étoiles à 0.001 seconde d'arc
près et 1 050 000 étoiles entre 0.007’’
et 0.03’’
On est loin du catalogue de 1005 étoiles établi en
1602 par Tycho Brahé, avec une précision avoisinant
les 30 secondes d'arc !

Tycho Brahé à la fenêtre de sa chambre
3. La parallaxe spectroscopique :
Lorsque les astrophysiciens ont commencé à analyser
le spectre de la lumière émise par les étoiles,
ils ont eu l'idée de s'en servir pour déterminer de
manière indirecte la parallaxe de ces dernières :
la classification stellaire permet en effet, à partir de l'analyse
spectroscopique, d'attribuer une magnitude absolue (= l'éclat
absolu de cette étoile si elle était placée
à 10 Parsecs de la Terre) à l'étoile étudiée.
Il suffit alors de mesurer le décalage entre cette magnitude
absolue et la magnitude apparente observée au télescope
pour connaître la distance de l'étoile, en utilisant
l'équation de Pogson m - M = 5 Log (d) - 5 où "m"
est la magnitude apparente de l'étoile vue au télescope,
"M" sa magnitude absolue, et "d" sa distance.
L'étalonnage de cette méthode se fait à partir
des étoiles les plus proches de la Terre pour lesquelles
on a pu calculer directement la parallaxe par la simple observation
visuelle. A partir de cet étalonnage, de proche en proche,
on a pu estimer la distance de nombreuses étoiles situées
au-delà. Cette méthode a cependant une limite : elle
ne marche que si l'on parvient à isoler la lumière de l'étoile
de celle de ses voisines afin de pouvoir en identifier le spectre.
4. L’utilisation du diagramme de
Hersprüng-Russel :
Cette méthode, également appelée méthode
de l'ajustement de la séquence principale, est plus récente
et est employée pour calculer la distance des amas d’étoiles.
Tout d'abord, rappelons ce qu'est le diagramme inventé par
Messieurs Hersprüng et Russel : ces derniers se sont rendus
compte qu'en mesurant la magnitude (= l'éclat) des étoiles
et en décomposant leur lumière au moyen d'un prisme,
on pouvait les classer selon le schéma ci-dessous.
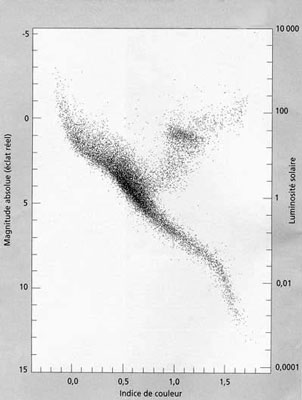
L'échelle verticale de gauche permet de classer les étoiles
en fonction de leur magnitude et celle de droite en fonction de
leur luminosité comparée à celle du Soleil
(1 correspond à la magnitude solaire). L'échelle horizontale
permet de classer les étoiles en fonction de la couleur de
leur spectre lumineux. Cette échelle horizontale peut aussi
être établie en fonction de la température des
étoiles. Chaque petit point du diagramme ci-dessus correspond
à une étoile, classée selon les critères
précédents.
Que constate-t'on donc ? Que la majeure partie des étoiles
suit, grosso modo, une diagonale que les astrophysiciens appellent
la "séquence principale". En clair, toutes les
étoiles de cette séquence principale, obéissent
à une loi toute bête : les plus lumineuses, en haut
et à gauche de la diagonale, sont aussi les plus chaudes
et les plus bleues. Inversement, plus une étoile est rouge
et moins elle est lumineuse.

Une exception : les étoiles géantes et super-géantes
rouges, qui forment un petit groupe d'étoile à part,
très rouges mais très lumineuses, à droite
de la séquence principale.
La séquence principale correspond à l'immense majorité
des étoiles de notre galaxie : ce sont des étoiles
arrivées à maturité, comme notre Soleil. Le
groupe des géantes rouges correspond aux étoiles arrivées
à la dernière phase de leur vie, avant qu'elles n'explosent.
Ce classement des étoiles de la galaxie selon le diagramme
de Hersprüng-Russel peut être utilisé pour évaluer
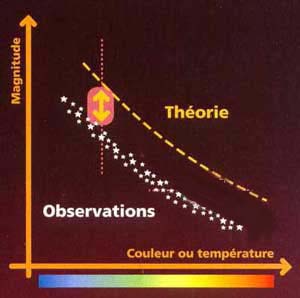
la distance de amas d'étoiles. Cette méthode consiste
à superposer sur un diagramme Hersprüng-Russel les points
représentatifs des étoiles de l'amas étudié
ainsi que les valeurs théoriques des étoiles de la
séquence principale de notre galaxie. Si on note un décalage
dans le sens vertical, c'est que la magnitude apparente observée
est décalée par rapport à la magnitude réelle
théorique : plus une étoile est lointaine et plus
sa magnitude est affaiblie par la distance. La mesure de ce décalage
entre magnitude théorique et magnitude observée permet
de déduire la distance de l'amas d'étoiles.
Si vous n'avez rien compris, ce n'est pas grave, on vous aime quand
même ...
5. Les Delta-Céphéides :
C'est à la grande astrophysicienne Henrietta
Leavitt que l'on doit la découverte d'étoiles
très bizarres, les Céphéides, dont le premier
exemplaire découvert a été l'étoile
Delta de la constellation de Céphée.

Pour en savoir plus sur les malheurs de cette grande
dame , cliquez sur sa photo
Ces drôles d'étoiles ont la particularité d'être
des étoiles variables dont la luminosité, (= la magnitude,
pour les astronomes) varie dans le temps avec une régularité
de métronome.
Cette bizarrerie est due à un phénomène physique d'une
permanence constante.
Toutes les étoiles connaissent un équilibre plus
ou moins stable entre, d'une part, la pression des rayons lumineux
qui s'échappent du coeur de l'étoile (les astronomes
parlent de pression radiative) et, d'autre part, la gravitation
de l'étoile qui tend à tasser celle-ci sur elle-même.
Dans le cas des Céphéides, lorsque la pression radiative
au coeur de l'étoile devient majoritaire, sa température
s'accroît et elle se dilate. La luminosité d'une étoile étant
fonction du volume de l'étoile et de sa température, l'éclat de
la Céphéide tend alors à augmenter.
Mais si la Céphéide se dilate, sa surface augmente
en proportion, ppermettant une dissipation plus rapide des rayons
issus du coeur de l'étoile : cette dissipation plus importante
entraîne une baisse de la température de la Céphéide.
La force de gravitation va alors pouvoir reprendre le dessus, et
l'étoile se contractera à nouveau. Une fois refroidie et
diminuant de volume, son éclat s'affaiblit. Comme la masse de l'étoile
est restée pratiquement identique durant tout c eprocessus,
le cycle pourra recommencer selon les mêmes conditions, donc dans
les mêmes temps pour chaque phase, ce qui explique la constance
dans le temps et la variation d'éclat des Céphéides.
A chaque cadence de pulsation correspond une magnitude bien précise,
et vice-versa.
Henrietta Leavitt et son collègue Harlow Shapley ont eu
l'idée, en 1918, de se servir du comportement bizarre des
Céphéides pour mesurer leur distance.

Harlow Shapley sortant de chez le coiffeur
Leur méthode est très astucieuse. Lorsqu'on observe
au télescope une Céphéide, on peut mesurer
sa magnitude apparente : plus une étoile est éloignée
et moins elle est brillante. S'il s'agit d'une Céphéide,
sa luminosité pulse dans le temps. En mesurant la cadence
de ces pulsations, on sait à quel type de Céphéide
on a affaire, et donc on peut connaître sa magnitude absolue
(la magnitude absolue est la magnitude qu'aurait l'étoile
si on la plaçait à 10 Parsecs de la Terre).
Il n'y a plus qu'à calculer la différence entre
la magnitude absolue et la magnitude apparente observée pour
en déduire la distance à laquelle se trouve la Céphéide.
Elémentaire mon cher Watson !!!
Cette méthode est très efficace pour mesurer la distance
des Céphéides qui se trouvent dans les amas globulaires
d'étoiles en orbite autour du noyau de la Voie Lactée,
ou bien pour calculer la distance des galaxies voisines de la nôtre.
Mais plus une galaxie est lointaine, et plus cette méthode
est délicate à mettre en oeuvre, car il faut commencer
par y repérer une Céphéide dont la luminosité
soit suffisante. Ensuite, il faut réussir à identifier
son rayonnement et le distinguer de celui des étoiles voisines
si l'on veut parvenir à en mesurer la magnitude apparente
: tout celà devient assez coton dès que les galaxies
sont un peu trop éloignées de nous.
A défaut de Delta-céphéide, on peut se rabattre
sur un autre type d'étoile variable, les RR Lyrae. Mais la
régularité de leurs pulsations est beaucoup moins
précise que celle des Céphéides et, par conséquent,
elles donnent des mesures de distance beaucoup moins fiables.
6. Les Supernovae :
Certaines étoiles ont la particularité de finir leur
jours en explosant en une Supernova. Il existe parmi ces Supernovae
un groupe bien spécial, les SN Ia, qui a la particularité
d'exploser en un temps bien précis.
Les SN Ia ont la particularité d'avoir toute la même magnitude
absolue. Cela résulte de ce qu'elles explosent lorsqu'elles atteignent
très exactement 1,4 masses solaires. Ce sont toutes des étoiles
naines blanches affublées d'un compagnon à qui elle piquent de la
matière par gravitation. il existe une limite, dite limite de Chandrashekar
(le gus qui a eu le Nobel pour ça, en 1983 si je me souviens bien...)
au-delà de laquelle l'étoile naine blanche ne peut
plus se goinfrer de matière provenant de sa voisine. Dès
que cette limite est atteinte, la naine blanche explose aussi sec
en Supernova... Bien fait, la gourmandise est un vilain défaut.
Bref, ça pète dans une condition bien précise, avec la même luminosité,
et donc toujours la même magnitude absolue. Une aubaine pour les
arpenteurs du ciel : les astrophysiciens peuvent alors se servir
de l'écart entre cette magnitude absolue et la magnitude
apparente qu'ils constatent dans leur télescope pour estimer
la distance à laquelle se trouve la Supernova.
Actuellement, des recherches ont lieu sur un utilisation encore
plus audacieuse des Supernovae, en se servant de la théorie
de la relativité d'Albert Einstein, qui a prévu que
le temps se dilate, s'allonge pour les grandes distances.

De fait, on constate que l'explosion de certaines Supernovae très
lointaines dure plus longtemps qu'on ne le prévoyait. Une
hypothèse pourrait être celle selon laquelle la durée
de l'explosion semblerait allongée du fait de la dilatation
de l'espace-temps, conformément à la loi de la relativité.
A grand renfort d'équations biscornues, on pourrait ainsi
estimer l'éloignement de cette Supernova, et donc de la galaxie
qui l'héberge, grâce à cette dilatation du temps
de l'explosion de la Supernova.

Une Supernova vient d'exploser dans cette galaxie, en bas et à
gauche de la photo
7. La méthode Tully-Fisher :
Tout récemment, en 1977, les astronomes Tully et Fisher
sont parvenus à établir qu'il existe une relation
mathématique entre la vitesse de rotation des galaxies sur
elles-mêmes et leur magnitude absolue. On sait en effet que
la période de rotation d'une galaxie spirale est fonction de sa
masse. Par ailleurs, il existe également une relation mathématique
entre sa masse et sa luminosité. Tully et Fisher en ont donc conclu
qu'on pouvait estimer la magnitude absolue de ce type de galaxie
à partir de sa vitesse de rotation.
Grâce aux radiotélescopes, on peut estimer cette vitesse
de rotation dans les grandes longueurs d'ondes, en particulier les
longueurs d'ondes radio (Cocorico, la France possède à
Nancay l'un des plus grands radiotélescopes du monde !!!).
La formule de Tully-Fisher donne alors la magnitude absolue M de
la galaxie. Parallèlement, avec un photomètre, il
est possible de mesurer la magnitude apparente de la galaxie étudiée.
Il ne reste plus alors qu'à comparer la magnitude absolue
et la magnitude apparente observée pour en déduire
la distance de la galaxie.
Cette méthode, élégante, souffre cependant
quand même d'un gros défaut : pour être précise,
la formule de Tully-Fisher doit être étalonnée
de façon exacte. Cet étalonnage ne peut se faire que
sur des galaxies dont on connait bien la distance exacte. Et ce
genre de bêtes-là ne sont pas foule ... Que la distance
des galaxies-étalons soit remise en cause et tout le calibrage
de la formule de Tully-Fisher est à reprendre à zéro
!
Deuxième écueil : cette formule magique ne s'applique
qu'aux galaxies spirales, dont la population d'étoiles est
suffisamment homogène pour que les relations masse / luminosité
et masse / vitesse de rotation restent valables . Les autres galaxies,
dont la population d'étoiles est beaucoup plus hétéroclite,
ne permettent pas d'utiliser la formule de Tully-Fisher.

8. Et demain ?
Aussi précis soit-il, le catalogue du satellite Hipparcos
reste encore entâché d'incertitudes. Un exemple tout
bête : le magnifique amas d'étoiles des Pléiades
serait distant de 378 Années Lumière selon Hipparcos
mais de 424 Années Lumière selon la méthode
des ajustements ...
Pour affiner les résultats d'Hipparcos, les astrophysiciens
envisagent de mettre en orbite dans les années à venir
un nouveau satellite, infiniment plus puissant qu'Hipparcos : le
projet Gaïa.
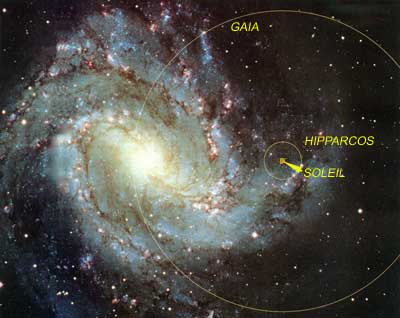
Schéma montrant la place de notre Soleil dans notre galaxie,
la zone explorée par Hipparcos et celle qu'explorera le futur
satellite Gaïa. |