Pour reproduire l'expérience d'Eratosthènes, les
deux clubs d'astronomie ou les deux écoles participants doivent
être séparés d'au moins 4 degrés de latitude.
Pourquoi ? Parce qu'un correspondant situé à 4 degrés au sud de
votre ville mesurera un angle inférieur de 4 degrés à celui que
vous mesurerez le même jour.
Malheureusement, les mesures que vous allez faire ne sont qu'une
estimation de l'angle réel entre le Soleil et la verticale. Comme
vous vous en doutez, cette estimation est nécessairement entachée
d'erreur. Tantôt, vous mesurerez un angle supérieur à la réalité,
tantôt inférieur. Cet écart, cette erreur dépend à la fois de la
qualité de votre gnomon (longueur et "perpendicularité" du stylet),
et de la qualité de sa mise en station (horizontalité de la planche,
tracé du méridien local). Vous aurez bien sûr compris que votre
objectif est de faire une mesure aussi précise que possible.

Si l'erreur que vous commettez sur chaque mesure est de 3 à 4 degrés,
il est évident que votre calcul du tour de la Terre sera très éloigné
de la réalité puisque cette erreur est justement égale à la différence
entre votre mesure et celle de votre partenaire. Si vous arrivez
à faire une mesure fiable à 2 degrés près, c'est mieux mais votre
partenaire ayant à peu près la même précision, il y a encore un
fort risque que la différence de vos mesures s'annule ! En conclusion,
il est donc nécessaire que votre gnomon soit suffisamment bien réglé
et bien installé pour vous permettre de faire des mesures avec une
précision de (au moins) 1 degré.

Nous avons voulu regrouper dans cette fiche un ensemble de conseils
et d'idées pour vous aider à améliorer la précision
de vos mesures
Des erreurs à répétition !
À chaque fois que vous assemblez deux parties de votre instrument
ou que vous installez votre instrument avant une mesure, vous commettez
inexorablement de petites erreurs qui, mises bout à bout, pourraient
bien fausser votre mesure. Parfois celles-ci se compensent par chance,
parfois elles s'ajoutent et nuisent gravement à vos relevés, alors
il est bon de contrôler toutes les étapes avec la plus grande minutie.
Faites donc la liste avec tous les participants à l'expérience
des différentes étapes qui ont mené à chaque mesure, depuis l'assemblage
de votre gnomon :
choix et mesure de la longueur du stylet
fixation de cette tige perpendiculairement à la planche qui est
elle-même sensée être parfaitement plane
installation de la planche et vérification de son horizontalité
tracé du méridien et repérage du passage de l'ombre du stylet sur
la ligne méridienne
mesure de cette ombre
tracé du secteur angulaire grâce aux longueurs de l'ombre et du
stylet
mesure de cet angle.
Il vous faut maintenant admettre qu'à chacune de ces étapes, vous
avez fait une faible erreur. Vous comprenez que la mesure finale
et donc le calcul du diamètre terrestre peuvent être très éloignés
de la réalité ! Comment réduire au maximum l'erreur de mesure sur
un angle ?
En augmentant au maximum les longueurs des côtés que vous tracez
pour mesurer cet angle. En effet, on ne peut jamais connaître exactement
une longueur, mais on la mesure avec une certaine précision (donnez
un double décimètre à 3 personnes successivement et demandez-leur
de mesurer la taille de votre bureau au demi-millimètre près : ils
trouveront à coup sûr 3 mesures différentes !).
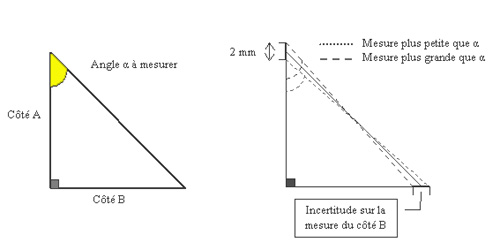
Supposons maintenant que vous souhaitiez mesurer l'angle alpha
représenté sur la figure ci-dessous à partir de la connaissance
des longueurs des segments A et B. Supposons (ce qui est raisonnable)
que les longueurs de A et B ont été mesurées à ± 1 mm. La figure
vous montre que ces incertitudes sur les longueurs A et B entraînent
une incertitude sur la connaissance de l'angle alpha lui-même.
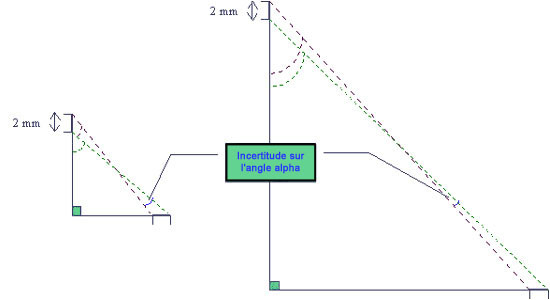
Pour réduire cette incertitude, triplez ou quadruplez les longueurs
A et B. L'incertitude sur la mesure de leur longueur, elle, reste
la même (elle ne dépend que de votre façon de mesurer : qualité
de votre règle et de votre lecture). Par contre, l'incertitude sur
l'angle diminue. La figure 2 devrait vous en convaincre : remarquez
les angles extrêmes dus à ces incertitudes, ils marquent les limites
qui encadrent la valeur réelle de l'angle alpha : ici 45 degrés.
Cet intervalle diminue bien sur la figure la plus grande (vérifiez
avec votre rapporteur !). Ainsi, vous avez tout intérêt à utiliser
de grandes longueurs pour mesurer les angles.
Applications :
Utilisez de préférence de grands instruments : équerre pour vérifier
que votre gnomon est bien perpendiculaire à la planche. Attention
: il faut le vérifier dans deux directions perpendiculaires l'une
par rapport à l'autre, c'est-à-dire tourner de 90 degrés autour
du pied du gnomon et contrôler à nouveau dans cette nouvelle direction.
En effet, le gnomon peut être incliné dans n'importe quelle direction
!
Un gnomon plus long sera plus facile à installer bien perpendiculairement
à la planche, cependant s'il dépasse 20 cm, son ombre deviendra
vite floue, même au midi solaire. Privilégiez donc un gnomon d'une
dizaine de cm Si vous avez réalisé un niveau à bulle pour contrôler
l'horizontalité de votre planche, il sera d'autant plus précis que
la surface de liquide est grande, d'après le principe expliqué précédemment.
Utilisez de préférence des crayons à mine très fine (type critérium)
pour tracer les longueurs mesurées, vous réduirez ainsi les erreurs
de lecture des angles. De même, servez vous plutôt de rapporteurs
de grande taille pour lire l'angle final, vous atteindrez ainsi
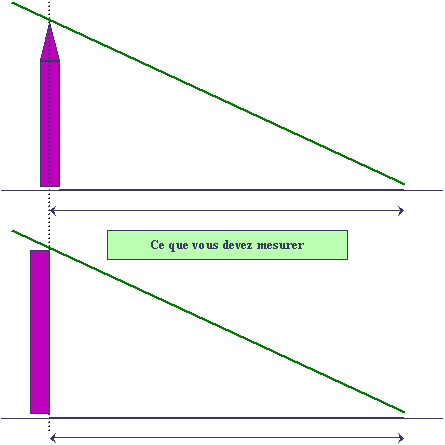
une plus grande précision dans la lecture. Remarque : selon la forme
de votre gnomon (pointu ou plat à l'extrémité), il vous faudra mesurer
la longueur de l'ombre à partir de points différents à son pied,
observez bien la figure ci-dessous car vous risquez d'introduire
systématiquement une erreur dans vos relevés.
Évaluez vous-même la précision de vos mesures :
Pour avoir une idée de la précision de vos mesures, c'est très
simple : il vous suffit de faire des relevés tous les jours. D'un
jour sur l'autre, la valeur de l'angle des rayons solaires par rapport
à la verticale varie très peu (entre 0,2 et 0,1 degré par jour à
partir de mi-mai). Suffisamment peu, donc, pour que vous ne puissiez
le remarquer dans vos mesures. Ainsi, en faisant trois mesures trois
jours de suite, vous aurez une idée des erreurs aléatoires que vous
faites lors du réglage de votre instrument et de votre mesure. Vous
obtiendrez trois mesures qui doivent être aussi semblables que possible.
En revanche, vous ne pourrez pas connaître votre erreur par rapport
à la valeur "réelle" de l'angle que vous mesurez.
Bon courage à tous, vous avez presque atteint votre but !
Complément :
Voici la description d'un gnomon réalisé par les élèves
d'une classe d'école primaire. Ce gnomon, très simple dans
sa conception, donne d'excellents résultats ! Pour la réalisation
du gnomon, rien de bien original : un plateau en agglo mélaminé
posé sur une table et sur un des chants du plateau une tige en bois
dépassant de 10 cm, de section ronde (8 mm), serrée (pas trop pour
que les enfants la réajustent à tout moment) par un collier pour
tube de cuivre (de plomberie). Pour chaque mesure, il y a un vérificateur
de l'horizontalité du support et de la verticalité du gnomon, un
enfant trace sur le plateau l'extrémité de l'ombre et une équipe
de retour en classe est chargée de passer à l'action (tracer le
fameux triangle et mesurer l'angle du jour...).

|