ERATOSTHENES

Un géographe de génie :

Eratosthènes (275 - 195 avant JC) était un géographe hors pair. Après avoir étudié 20 ans durant dans la célèbre Académie créée à Athènes par Platon, Eratosthènes était devenu un touche-à-tout de génie : éditeur des oeuvres d'Archimède, philosophe, musicien, astronome, poète, géographe, il disposait de plusieurs cordes à son arc !

D'ailleurs, c'est même lui qui a inventé le mot "géographie" (géo = la Terre, graphein = dessiner en grec). On lui doit en particulier la première carte de géographie fiable de toute l'histoire de l'humanité.

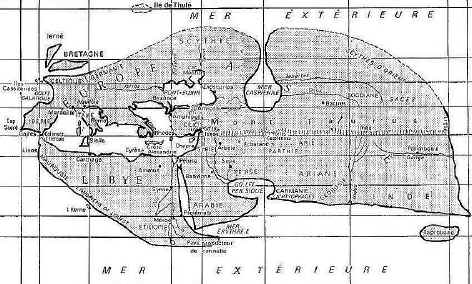
La carte d'Eratosthènes

La réputation d'Eratosthènes était telle que le roi d'Egypte Ptolémée VIII Evergète lui confia vers 235 avant JC la direction de la plus célèbre bibliothèque du monde antique : la bibliothèque d'Alexandrie.

Le temple de Philae

C'est dans cette bibliothèque fabuleuse qu'Eratosthènes devait trouver un trésor : les journaux de toutes les campagnes guerrières effectuées un siècle plus tôt par le conquérant grec Alexandre-le-Grand, ainsi que les notes des philosophes et des savants qui l'avaient accompagné dans ses aventures.

Devant l'immensité des conquêtes d'Alexandre-le-Grand, une question a forcément germé dans la brillante cervelle d'Eratosthènes : tout celà, ces mers, ces montagnes, ces cités, cette immense vallée d'Egypte, en un mot la Terre, celà mesure combien ?

Ombre et lumière en Egypte :

Eratosthènes avait entendu dire par des voyageurs, qu'à midi, le jour du solstice d'été à Syène, au Sud de l'Egypte, le Soleil était tellement haut dans le ciel que son reflet tombait tout au fond d'un puits et qu'un bâton (=gnomon en grec) planté verticalement dans le sol ne faisait aucune ombre sur le sol.

Or, dans la ville d'Alexandrie, il n'en était pas de même : en regardant l'obélisque, Eratosthènes constata que le jour du solstice d'été, à midi, cet obélisque possédait une ombre. Même constatation avec un gnomon planté verticalement dans le sol.

Eratosthènes était donc confronté à une terrible énigme : le même jour, à midi, pas d'ombre à Syène et une ombre à Alexandrie. Pourquoi ?

Deux hypothèses logiques s'offraient alors à Eratosthènes. Première hypothèse : la Terre est plate et le Soleil en est très proche et, de ce fait, ses rayons frappent le sol de manière divergente.

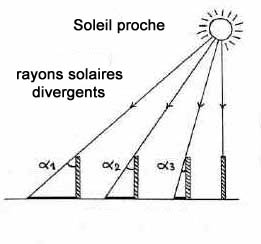
Deuxième hypothèse : le Soleil est infiment loin de la Terre et de ce fait, ses rayons sont à peu près parallèles. Si la surface de la Terre n'est pas plate mais courbe, alors la différence d'ombre entre Syène et Alexandrie peut s'expliquer. Et si la surface de la Terre est courbe, ce ne peut être que parce que la Terre elle-même est ronde. C'est cette deuxième hypothèse qu'Eratosthènes choisit.

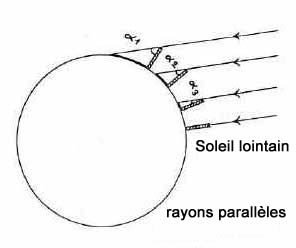
Certes, plusieurs philosophes avaient déjà avancé cette hypothèse dans le passé, comme Pythagore qui faisait remarquer qu'un marin perché en haut du mât de son bateau voyait plus loin que l'horizon du marin resté sur le pont. De même, Aristote avait également remarqué lors des éclipses de Lune que l'ombre de la Terre est ronde, ce qui semblait indiquer que la Terre n'est pas plate.

Mais c'est Eratosthènes qui devait en apporter la preuve irréfutable, grâce à son sens de l'observation et grâce à la puissance de son intelligence.

Rock around the gnomon :

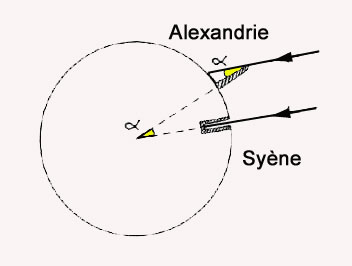
Si la Terre est ronde, alors, forcément, deux gnomons plantés l'un à Alexandrie et l'autre à Syène doivent se couper au centre du globe terrestre, si on les prolonge par la pensée.

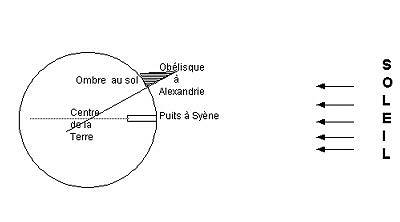
Et en ce cas, puisque les rayons du Soleil sont parallèles, Eratosthènes se dit que l'angle "alpha" au centre de la Terre entre l'obélisque d'Alexandrie et le puits de Syène, doit être égal à l'angle que fait l'ombre de l'obélisque d'Alexandrie. Allez, cherchez donc un peu dans vos souvenirs de l'école primaire : les angles "alpha" sont tout bêtement les deux angles internes d'une sécante de parallèle. Vous n'avez quand même pas déjà oublié çà, non ?

Le coup de pouce de Thalès de Milet :

A partir de ce raisonnement géométrique lumineux, tout s'enchaîne très vite pour Eratosthènes qui, en 205 avant JC, décide de mesurer cet angle "alpha"

Pour ce faire, Eratosthènes reprend le théorème attribué par la tradition orale à l'un des 7 sages de la Grèce Antique, Thalès de Milet. Car Thalès de Milet, était venu, lui aussi, se balader en Egypte où il aurait réussi la performance de calculer la hauteur de la Grande Pyramide de Khéops sans la mesurer directement. Thalès aurait tout simplement remarqué que le rapport entre la taille d'un gnomon et son ombre était exactement le même que le rapport entre l'ombre de la pyramide et sa hauteur. Cette constatation devait passer à la postérité sous le nom de "théorème des triangles semblables", théorème que vous avez forcément appris à l'école primaire sous le nom de "théorème de Thalès". C'est probablement là le premier théorème mathématique de toute l'histoire de l'Humanité.

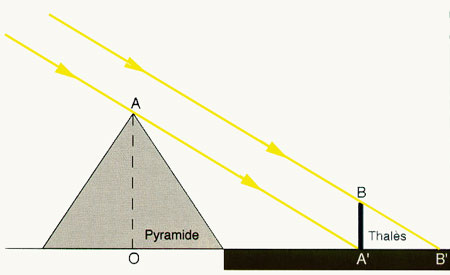
Les triangles AOA' et BA'B' sont semblables, donc AO / BA' = OA' / A'B'
par conséquent, la hauteur de la pyramide AO est égale à BA' x OA' / A'B'

L'époustouflante démonstration d'Eratosthènes :

Armé de ce précieux théorème, Eratosthènes peut alors s'attaquer à la mesure de la circonférence de la Terre. Il découvre que l'angle "alpha" est à midi, le jour du solstice d'été à Alexandrie, de 7 degrés.

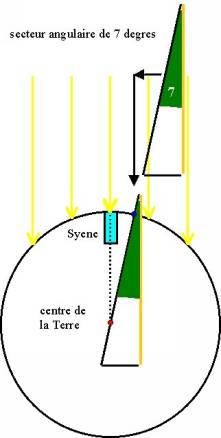
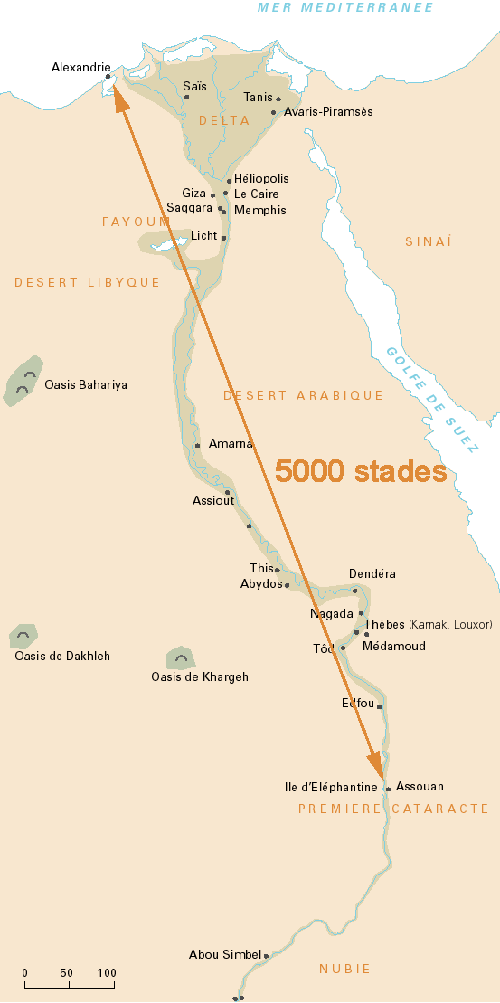
Or, 7 degrés, celà équivaut à la 50ème partie de la circonférence d'un cercle. Il ne reste plus alors à Eratosthène qu'à se faire une petite multiplication : estimant, d'après la longueur des voyages des caravanes de chameaux, que Syène et Alexandrie sont distantes de 5000 stades égyptiens (soit 157,5 mètres), il n'a plus qu'à multiplier 5000 stades par 50 pour avoir le tour de la Terre, soit 250 000 stades. Soit 39 735 kilomètres. A 10 % près, c'est effectivement la circonférence de la Terre. Impressionnant ... L'erreur vient essentiellement du fait que la distance exacte Syène - Alexandrie n'est pas de 5000 stades, soit 787,5 km mais en réalité de 701 km. Mais bon, on ne chipotera pas !!!

L'oubli :

Malheureusement, l'éblouissante découverte d'Eratosthènes devait se perdre peu à peu dans les sables de l'histoire, en particulier à cuase des guéguerres que se livrèrent avec acharnement les différents successeurs d'Eratosrthènes.

Déjà, Eratosthènes lui-même avait porté un premier coup de canif dans sa superbe démonstration, en décidant arbitrairement de porter la circonférence de la Terre à 252 000 stades afin qu'un degré de méridien mesure exactement 700 stades. Eratosthènes était comme çà : il aimait les beaux chiffres bien ronds. Comme quoi, on peut être un génie et aimer tripatouiller une drôle de cuisine ... cependant cet "ajustement" ne faussait pas le résultat de façon conséquente puisque l'erreur expérimentale due à la technique du gnomon est de toute façon supérieure à cet "ajustement".

C'est à la mort d'Eratosthènes, en 195 avant JC, que le jeu de massacre a réellement commencé, du fait de ses successeurs. C'est tout d'abord Posidonius de Rhôdes (135 - 50 avant JC) qui décida de réduire arbitrairement la taille de la Terre afin de ramener ses proportions à celles du monde antique connu.

Puis, un siècle plus tard, l'astronome Claude Ptolémée (90 - 168 après JC) reprit ces mesures bidonnées dans son ouvrage "l'Almageste". Et c'est cette carte allègrement traficotée qui fut reprise par les atronomes arabes qui la transmirent ensuite à l'Occident chrétien.

Et c'est cette carte qui donna enfin à un certain Christophe Colomb l'idée de traverser l'Océan Atlantique pour rejoindre les Indes : le chemin ne lui semblait en effet pas bien long à effectuer ... En fait, le voyage dura infiniment plus longtemps que prévu, et c'est en Amérique que Christophe Colomb toucha terre ... mais ceci est une autre histoire ...

Si vous souhaitez en savoir plus sur la découverte d'Eratosthènes, vous pouvez vous connecter au site ouaibe de l'Institut National de la Recherche Pédagogique et de l'association "La main à la pâte" créée par le prix Nobel J. Charpak. Pour mieux comprendre notre Terre et les mouvements apparents du Soleil dans le ciel, nous vous conseillons également le livre très richement illustré "Les saisons et les mouvements de la Terre", de Pierre Causeret et Liliane Sarrazin, édité chez Belin dans la collection "Pour la science". Pour plus de précisions, cliquez sur chacune des vignettes ci-dessous.