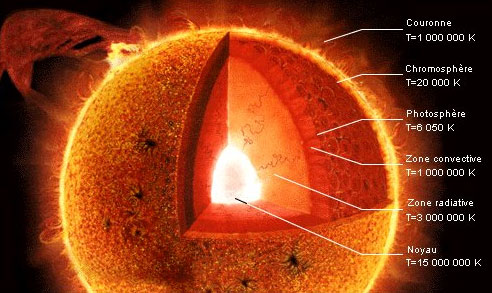
Au coeur du Soleil règne une écrasante densité due à la
force d'attraction générée par l'énorme masse
de notre étoile. Cette densité est tellement importante
qu'elle oblige les atomes à fusionner selon le schéma suivant
:
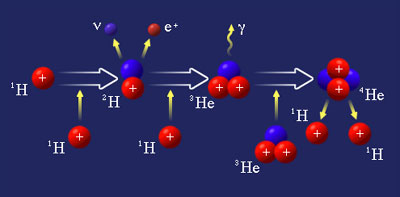
Mais entrons dans le détail de cette partie de billard thermo-nucléaire
dont nous distinguerons les différentes étapes :
- première étape : 2 atomes d'hydrogène H1 entrent
en collision pour former un atome de deutérium H2. Dans ce processus,
l'un des protons du noyau de l'hydrogène se transmute en un
neutron d'une part, et en émettant, d'autre part un positron
e+ et un neutrino.
- deuxième étape : le positron trouve rapidement un électron
libre e- avec lequel il va entrer en collision. Durant cette collision,
les deux petites particules vont s'annihiler en émettant un
photon gamma hautement énergétique. Il s'agit là de
la première explosion d'énergie qui suit le démarrage
des réactions de fusion thermo-nucléaires. Quant au neutrino,
il va s'éloigner à la vitesse de la lumière. L'un
des grands enjeux de l'astrophysique solaire moderne est justement
de comprendre ce que deviennent ces neutrinos fabriqués au coeur
du Soleil
- troisième étape : l'atome de deutérium fabriqué lors
de la première étpae de la fusion thermo-nucléaire
va à son tour entrer en collision avec un autre atome d'hydrogène
H1. Cette nouvelle collision va donner naissance à un atome
bizarre, l'hélium He3 dont le noyau est formé de 2 protons
et d'un seul neutron. La naissance de l'atome de He3 émet un
nouveau rayon gamma
- quatrième étape : cette nouvelle étape voit
la collision et la fusion de deux atomes de He3. De celle-ci va naître
un atome d'hélium stable, le He4, ainsi que deux atomes d'hydrogène
H1
Pour résumer toute cette réaction en chaîne a mis
en jeu un total de 6 atomes d'hydrogène H1. Au fil des transmutations
et collisions, cette réaction a finalement libéré 2
atomes d'hydrogène, 1 atome d'hélium, 2 neutrinos et 4
photons gamma hautement énergétiques.
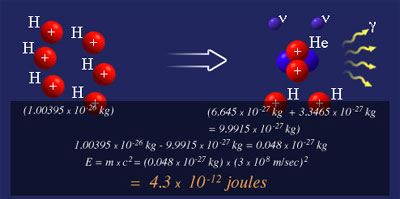
L'équation d'Einstein E = MC² est ainsi respectée,
les atomes d'hydrogène manquants ayant été convertis
en énergie sous forme de photons gamma.

Mais que vont donc devenir les photons gamma émis ? Ces photons
vont interagir avec le milieu ambiant qu'ils vont rencontrer au fur et à mesure
de leur déplacements au sein du Soleil. La longueur d'onde de
ces photons va alors se modifier en raison de la "perte" d'énergie du
photon incident qui en cède une partie à l'atome avec lequel il a interagi.
Ce dernier voit son niveau d'énergie augmenté de l'exacte quantité égale à la
différence entre l'énergie du photon incident et celle du photon réémis.
Ce n'est donc que le nombre de "rencontres" que fera le photon gamma
(ou plutôt, lui et ses descendants) qui déterminera la longueur d'onde
du dernier de la descendance au moment ou celui-ci quittera la photosphère
du Soleil.
Statistiquement ce nombre de rencontres serait identique si tous les
photons partaient du même endroit, mais d'une part, le noyaux où naissent
les photons géniteurs les plus anciens n'est pas un point et, d'autre
part, la masse du Soleil tend à lisser le niveau moyen d'énergie par
l'homogénéisation de la température. L'étalement des points de départ
se retrouve dans l'étalement des longueurs d'onde à la sortie avec un
resserrement autour d'une longueur d'onde préférentielle à une température
homogène de surface (lieux des derniers échanges), aux accidents de surface
près.

La variation de densité du milieu traversé, si elle n'a pas d'incidence
sur les longueurs d'onde, joue tout de même un rôle clef dans cette affaire.
L'interaction d'un photon avec un atome avec réémission d'un autre photon
n'a pas grand chose à voir avec une partie de boules de billard. Quand
la boule de billard frappe la bande, l'angle réfléchi est égal à l'angle
d'incidence. Au niveau de la "géométrie quantique", la partie est bien
plus drôle : si l'on peut connaître l'angle de percussion du photon
sur l'atome qui passait par là, le malin qui peut dire la direction qui
sera prise par le photon réémis n'est pas encore né... Le photon réémis
prendra la tangente en fonction de la position précise qu'occupait l'électron
qui va changer d'orbite avec la différence d'énergie prélevée au photon
incident à ce moment. C'est-à-dire qu'il peut prendre n'importe quelle
autre direction, y compris celle qu'avait le photon incident, auquel
cas il va revenir dans la direction d'où il venait !
En toute logique, ces photons devraient osciller éternellement autour
d'un point moyen qui serait leur lieu de naissance originelle, et sans
jamais trouver la sortie ... ce qui serait bien embêtant, car nous
serions alors plongés dans le noir si aucun photon ne pouvait
s'échapper du Soleil... C'est là que la densité du milieu intervient.
Puisque les atomes sont plus espacés les uns des autres en s'éloignant
du centre du Soleil, chaque parcours de photon en direction de l'extérieur
sera plus long, en distance, qu'un parcours vers l'intérieur, avant qu'il
ne se fasse absorber par une nouvelle rencontre avec un atome de gaz.
Les segments du parcours vers l'extérieur étant statistiquement plus
longs que les segments vers l'intérieur, le dernier de notre dynastie
de photons finira par se retrouver dehors.

Ce raccourci ne tient pas compte d'un mécanisme induit qui génère une
très grande quantité de photons paresseux : à chaque échange,
nous n'avons parlé que du héros, le vigoureux photon, et de son fils
qui devenait le héros de l'épisode suivant. Mais l'atome rencontré par
le photon-père a vu augmenter son niveau d'énergie lors de cette
rencontre. De rencontres en rencontres, l'atome finit par saturer ! Ses électrons
vont se trouver dans un état de grande instabilité. Le
seul moyen pour cet atome de retrouver un équilibre consiste à lâcher
du lest en émettant un photon dont le niveau d'énergie
correspond au trop plein d'énergie perçu lors de ses collisions
avec les photons en provenance du coeur du Soleil. Bien évidemment,
ce trop plein d'énergie reste relativement modeste et, comparé aux
photons gamma provenant du noyau solaire, ce photon émis est peu énergétique,
et présente donc une longueur d'onde relativement longue. Ainsi,
les courbes de luminosité des étoiles, dont le Soleil, ne sont pas symétriques
autour de la longueur d'onde préférentielle, mais s'étale largement du
côté des photons les plus flemmards : ondes radio, ondes infra-rouges,
ce qui nous permet de bénéficier de la chaleur de notre étoile
|