Ptolémée et le Géocentrisme

La discipline toute particulière qu'est l'astronomie, inspira de nombreuses civilisations, à commencer par les Babyloniens au IIIème millénaire avant notre ère, pour qui les cieux restaient le reflet de la destinée des hommes.

Il fallut attendre l'avènement des Grecs et de leurs différentes écoles telles que celles de Platon, d'Aristote et d'Alexandrie dont faisait partie Ptolémée, pour qu'apparaissent les premières tentatives d'explication rationnelle du mouvement des astres.

Avec son livre «l'Almageste» et ses différentes mesures très précises Ptolémée donna une bouffée d'oxygène à l'astronomie.

I) Retour historique sur l'astronomie

Le cosmos qui fait un toit à la Terre a attiré naturellement la curiosité de l'être humain dès que celui-ci a été capable d'une réflexion soutenue. L'importance des mythes relatifs au ciel, aux astres, aux planètes, au Soleil et à la Lune dans les religions antiques et primitives témoigne de la place de choix qu'occupait le monde des phénomènes célestes. Les premières traces écrites de cet intérêt des hommes pour l'astronomie remonte aux Babyloniens (ou Chaldéens), établis au confluent du Tigre et de l'Euphrate : ils nous ont légué de nombreuses tablettes couvertes d'inscriptions cunéiformes aujourd'hui déchiffrées.

Ils étudièrent avec soin le mouvement des astres, dès le III ème millénaire avant JC, ils multiplièrent les observations et s'aperçurent très tôt que les planètes, le Soleil, la Lune parcourent sensiblement la même région du ciel : l'écliptique. Ils groupèrent les étoiles en constellations et ils établirent un calendrier fondé sur les phases de la Lune. Ils s'attachèrent à prédire soigneusement les éclipses de Lune et de Soleil, événements très redoutés à cette époque.

Prédire l'avenir des hommes et de leurs destinées a permis à l'astronomie chaldéenne d'atteindre un niveau remarquable :  ils croyaient que la destinée était inscrite dans les cieux et les étoiles; d'ailleurs l'observation des astres était réservée aux prêtres, fonctionnaires chargés d'annoncer d'après l'examen du ciel les événements intéressant l'Etat.

Il fallut attendre le VI ème siècle avant notre ère l'apport des Grecs et donc de Ptolémée pour que s'instaure progressivement une rationalité scientifique écartant magie, astrologie et surnaturel de l'interprétation des phénomènes célestes.

II) la vie de Ptolémée

(Ptolémée) Ptolémée Claude, un astronome, géographe et mathématicien grec qui faisait partie de l'école d'Alexandrie. En dépit de son influence dans l'histoire de l'astronomie, on sait très peu de choses sur sa vie, il ne nous est parvenu aucune biographie. Où il naquit, où il mourut reste un mystère. Il est probablement né dans la ville grecque de Ptolémaïs d'Hermias dans la province de Thébaïde en Haute Egypte, qui à cette époque appartenait à la Grèce, en l'an 90 ou 100. Il a résidé pendant un long moment à Canope à l'embouchure ouest du Nil où il mourut en 170 ou 180 après JC sans aucune certitude. Mais son prénom Claude permet de penser aussi qu'il était peut-être citoyen romain.

III) Les conceptions de Ptolémée sur le monde et l'univers, son système géocentrique

Son œuvre très étendue reste aujourd'hui connue surtout en géographie et en astronomie. Son livre «l'Almageste» est une vaste compilation des connaissances astronomiques et géographiques des Anciens. Ptolémée imaginait en particulier qu'une grande terre inconnue limitait l'océan indien vers les hautes latitudes et joignait l'Afrique à l'Asie orientale. Cette conception d'un immense continent austral sera conservée jusqu'à la Renaissance. D'ailleurs Mercator, mathématicien et géographe flamand, né à Rupelmonde en 1512 et mort à Duisburg en 1594, le portera sur sa carte et il sera vite le principal objectif de la découverte du monde après la reconnaissance de l'Amérique. (Mercator)

(Copernic) Ptolémée imaginait aussi que la Terre était fixe au centre de l'Univers et développa un système cosmologique ingénieux (dont on sait aujourd'hui qu'il est cependant faux) apte à rendre compte des mouvements astronomiques observés à son époque : le géocentrisme. C'est à partir de son ouvrage le plus célèbre «l'Almageste» que l'on trouve les principes qui furent à la base de cette astronomie antique. Ce modèle de l'univers s'imposa jusqu'à la Renaissance, où Copernic  le récusa pour essayer de proposer un nouveau système, l'héliocentrisme, où c'est le Soleil qui est au centre de l'univers au lieu de la Terre.

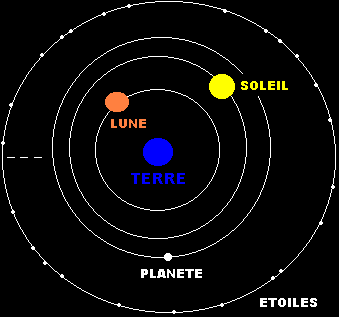
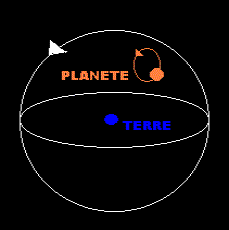
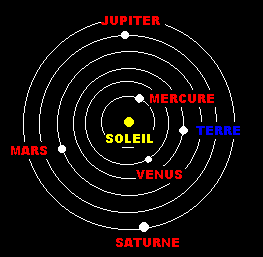
IV) Le système géocentrique de Ptolémée

Le système géocentrique

En fait, Ptolémée n'a fait que reprendre et systématiser des conceptions géocentriques antérieures à Aristarque car ce dernier (né à Samos en -310 et mort en -230) supposait à juste titre, 18 siècles avant Copernic, que la Terre tournait sur elle-même et autour du Soleil, mais ses idées furent rejetées comme impures.

Le système géocentrique de Ptolémée partait du principe que le cercle (une figure parfaite et divine) est le fondement de l'univers. La Terre est donc une sphère entourée d'une série de sphères de cristal concentriques, portant les différentes planètes et d’une sphère extérieure contenant les étoiles. Toutes ces sphères se meuvent à une vitesse constante. Chaque planète comme la Terre a une orbite circulaire autour d'un centre situé dans la sphère des planètes mais soumis lui-même à un mouvement circulaire appelé déférent.

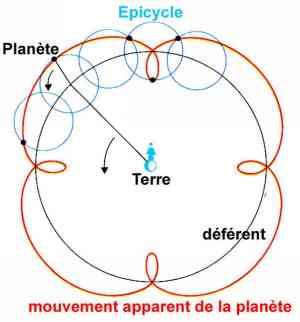
Ptolémée expliquait les saisons par des variations de la proximité du Soleil, l'orbite de celui-ci étant supporté par un épicycle dont le centre était entraîné le long de l'écliptique. Mais ce système ne permettait pas d'expliquer totalement ni les mouvements de la Lune ni les mouvements des planètes dans le ciel. 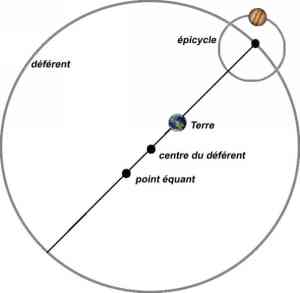Ignorant que les orbites de ces astres ne sont pas des cercles mais des ellipses, Ptolémée va réaménager son système d'épicycles pour essayer de le faire coïncider avec les phénomènes observés dans le ciel. Il va en particulier imaginer que les orbites des planètes forment des épicycles dont le centre est entraîné le long d'un cercle qu'il appelle déférent dont la particularité est que la Terre n'en est pas le centre : la Terre est un peu excentrée par rapport au centre du cercle déférent. A la position de la Terre correspond un point symétrique, appelé le point équant.

Pour calculer la taille de ses épicycles et ses déférents, Ptolémée utilisera, pour la première fois dans l'histoire de l'humanité, la technique du calcul par approximations successives à partir des positions des planètes dans le ciel au moment de leur opposition. La règle du jeu est assez simple : après avoir éliminé les données douteuses car trop imprécises, Ptolémée prenait ces données par trois afin de calculer les paramètres du cercle déférent, du point équant et de l'épicycle de chaque planète. Puis il reprenait un second paquet de 3 données, recommençait ses calculs, afin d'obtenir de nouveaux paramètres pour sa planète. Puis même manipulation avec un troisième paquet de données, Ptolémée écartant alors les paramètres qui divergeaient de manière trop importante. De proche en proche, Ptolémée finissait par ne garder que les paramètres les plus proches de la moyenne qui devenaient ainsi les paramètres de référence de la planète. Bien évidemment, cette méthode était totalement tributaire de la précision des mesures des positions des planètes dans le ciel.

Et malgré cette précision, les acrobaties sophistiquées du modèle de Ptolémée ne parvinrent jamais à expliquer tout à fait les mouvements des planètes ni à garantir leur prévision. C'est pourquoi l'univers géocentrique de Ptolémée finit par être remis en cause, par Copernic tout d'abord, qui émit l'hypothèse selon laquelle c'est le Soleil qui est au centre du système solaire, suivi par Galilée puis par Képler qui eût l'intuition géniale que les orbites des planètes n'étaient pas des cercles mais des ellipses et qui réussit, à partir de cette découverte, à calculer enfin avec exactitude les mouvements réels des planètes.

V) L'almageste et autres découvertes et inventions.

Jusqu'à la fin de l'Antiquité, l'ouvrage majeur de Ptolémée, «l'Almageste» fut appelé le «Mégiste syntaxis» en opposition à une autre œuvre mineure. Les Arabes ont transformé le titre en «Al-Majisti» qui fut traduit en latin par les moines du Moyen-Age sous le nom de «Almagistum».

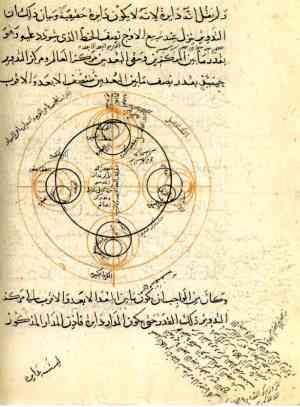L'Almageste est un traité qui comporte plusieurs livres, au nombre de 13. Les 2 premiers sont consacrés aux bases philosophiques et scientifiques sur lesquelles reposent toutes les autres théories de Ptolémée : en particulier on y découvre une conception de l'univers entièrement mathématique. Ptolémée y expose aussi la trigonométrie avec sa première fonction jusqu’alors unique dite « corde » utilisée à la place du sinus moderne.

La Terre est rigoureusement immobile, et se trouve au centre du système de Ptolémée. Ses dimensions sont négligeables par rapport à l'extension de l'univers. Il y a 2 cercles de références fondamentaux : l'équateur et écliptique,  qui se coupent selon un angle valant 11/83 ème de la circonférence, comme l'avait déjà calculé Erathostène et Hipparque. Le jeu de ces 2 cercles est la structure cardinale de l'astronomie ancienne. Ptolémée affirme dans ce livre que le mouvement de la sphère stellaire le long de l'équateur entraîne toutes les sphères planétaires qui cependant courent à l'oblique le long de l'écliptique.

Dans le second livre consacré au Soleil, Ptolémée propose de trancher entre un mouvement excentrique (trajectoires circulaires dont le centre bien que proche de la Terre ne coïncide pas avec celui-ci) et mouvement épicycloïdal (la trajectoire de la planète est la résultante de son mouvement circulaire uniforme autour d'un centre qui lui-même se déplace autour de la Terre). En mesurant la durée des saisons il trouva la même position du Soleil qu'Hipparque : une fois de plus les 2 mouvements apparaissaient équivalents. Il opta en définitive pour le mouvement excentrique car il ne nécessitait qu'une seule étape de calcul au lieu de deux.

Il n'en est pas de même pour la Lune traitée dans les 4^ème, 5^ème, 6^ème et 7^ème livres, dans la mesure où son apogée migre le long de l'orbite autour de la Terre. Il a été contraint d’adopter un système d'épicycles dont le déférent est excentrique (donc non centré sur la Terre).  Même si le modèle n’est pas adapté aux quadratures (le 1^er et dernier quartier de la lune) il décrit tout de même très bien les éclipses.

Les 8^ème et 9^ème livres traitent des étoiles et comprennent le plus ancien catalogue d'étoiles parvenu jusqu'à nous : une liste majestueuse de près de 1022 objets réunis en 48 constellations (12 pour le zodiaque, 21 dans l'hémisphère boréal et 15 dans l'hémisphère austral). Leurs positions sont mesurées avec une précision de 1/6 de degré près, et pour la première fois la magnitude des étoiles est subdivisée en 6 classes : la ou les 1^ères étoiles qui apparaissaient à la nuit tombante étaient classées comme de magnitude 1, puis les étoiles qui apparaissaient en second étaient classées de magnitude 2, etc... Ce catalogue date de 137 après JC.

Les 5 livres suivants concernent les planètes. Pour des cas aussi simples que Mercure et Vénus, Ptolémée prend des épicycles autour de la position du Soleil, leurs dimensions sont facilement calculées par les mesures angulaires de leurs élongations respectives.

Pour les autres, les choses se gâtent à cause de leurs mouvements en partie rétrogrades comme Mars par exemple.

Dans les 2 derniers livres, Ptolémée met en tableau les arcs, les orbites planétaires, les instants d'inversions du mouvement des planètes et les valeurs de la latitude écliptique.

Il conclut son œuvre avec le problème du lever et coucher héliaque des planètes (se dit du lever d'un astre qui a lieu peu avant celui du Soleil, et le coucher d'un astre peu de temps après celui du Soleil) des données d'un intérêt fondamental pour les prévisions astrologiques,  ce sur quoi on appuyait généreusement les observations astronomiques et les récits cosmogoniques.

D'autres titres de livres sont attribués à Ptolémée, avec plus ou moins de certitude, notamment «l'Analemme». Il a également travaillé sur l'optique, notamment sur la réflexion et la réfraction de la lumière, car les Grecs connaissaient le pouvoir grossissant du verre et sa capacité à concentrer les rayons du Soleil.

Ptolémée a inventé des instruments tels que l'astrolabe (instrument permettant d'obtenir pour une latitude donnée une représentation plane simplifiée du ciel à une date quelconque), ainsi que des planisphères et des globes célestes.

L'astrolabe

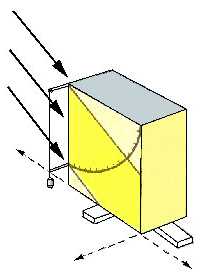
Instrument inventé par Ptolémée pour mesurer la hauteur du Soleil,
au moyen de l'ombre projetée par une baguette, d'un fil à plomb et d'une échelle graduée.

VI) L'école d'Alexandrie.

Pendant des centaines d'’années et ceci bien après la mort de Ptolémée, les philosophes et les astronomes ont rivalisé d'ardeur pour tenter de donner une explication et une description correctes de l'univers. Certes leur cosmologie restait très arbitraire mais contrairement à leurs prédécesseurs, ils ne s'en tiendront pas à de simples constatations, ils s'efforceront de comprendre du mieux qu'ils pouvaient le mouvement des astres, s'interrogeant sans cesse sur la distance des corps célestes et cherchant à déterminer les dimensions de la Terre, de la Lune et du Soleil. Pour ceci les différents philosophes, mathématiciens et astronomes ont fondé des écoles, comme Thalès (né à Millet en -636, et mort en -546), Pythagore (né en -585 à Samos et mort en -500), et ainsi de suite bien au-delà de la mort de Ptolémée.

Nous parlerons plus précisément de l'école d'Alexandrie dont faisait partie Ptolémée.

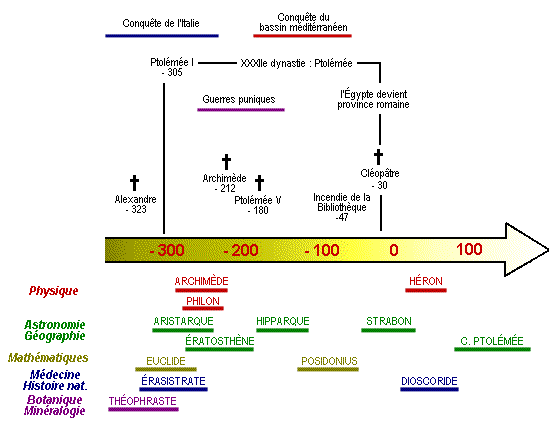
A la suite des conquêtes d'Alexandre Le Grand, la culture et la langue grecques pénètrent très largement en orient, et l'activité scientifique se concentre dans le sud du bassin Méditerranéen et tout particulièrement à Alexandrie. L'astronomie va durant cette période connaître un développement remarquable grâce à l'application combinée des mathématiques, de la mécanique, et de la technique.

Le premier représentant de l'école d'Alexandrie est Euclide ( né vers 300 av JC ).

(Euclide) Il inventa le plan euclidien, la théorie des nombres irrationnels, les éléments, les axiomes, le postulat, Euclide fut le synonyme de perfection.

Citons aussi Aristarque de Samos dont l’activité scientifique se situe aux alentours de 280 avant JC. Sa découverte essentielle fut d'être arrivé à mesurer le temps que met le disque lunaire à traverser l'ombre de la Terre lors d'une éclipse totale de Lune, grâce à quoi il parviendra à évaluer le rapport du rayon lunaire au rayon terrestre (à peu près 1/3). Avec une méthode de trigonométrie il essayera de comparer les distances de la Lune et du Soleil mais sans grand succès. Par contre il concevra quelques 17 siècles avant Copernic un système héliocentrique mais sa découverte n'eut aucun écho et fut tout simplement étouffée par la théorie géocentrique. Aristarque partagea sa place avec Archimède né en -287 à Syracuse et mort en -212, il fut le plus grand génie de ce temps.

La compétence d'Archimède fut universelle : calcul du volume d'un cylindre, de la sphère, calcul d'une valeur approchée, étude du système de levier,  la fameuse vis sans fin, la découverte du principe d'Archimède (tout corps plongé dans un liquide ou un gaz, reçoit une poussée vers le haut et qui est égale au poids du volume de liquide déplacé). Il fit même construire des machines de guerre. Avec ses inventions et ses découvertes il allie l'extrême rigueur au souci d'une application pratique. (Archimède)

(Eratosthène) A la même époque le géodésien Erathostène, né en -284 à Cyrène et mort en -192, mesure la longueur de la circonférence terrestre. Et sa découverte procédant d'une méthode juste (le principe des gnomons) permit aux astronomes alexandrins d'évaluer la distance de la Lune à la Terre, connaissant le rapport du rayon lunaire au rayon terrestre.

Mais c'est Hipparque qui remporte le titre de plus grand astronome de tous les temps dans l'école d'Alexandrie durant l'Antiquité. Il vécut au 2^ème siècle avant JC, il est né en -190, et mort en -125. Il eut l'idée de classer les astres par grandeur et dressa le premier catalogue d'étoiles. Il découvrit, en comparant ses propres observations à celles de ses prédécesseurs, la précession des équinoxes. Fondateur de la trigonométrie, il donna la théorie des mouvements de la Lune et du Soleil (bien avant Ptolémée) en expliquant en particulier le mécanisme des éclipses.

L'école d'Alexandrie a également compté dans ses rangs une femme (et oui !) : Hypathie, fille de Théon d'Alexandrie, savant du 4 ème siècle après JC. Erudite, elle diffusa des œuvres de mathématiques et d'astronomie, ce qui lui valut d'être lapidée en 415. Elle fut la dernière représentante de l'école d'Alexandrie. (Hypathie)

VII) La décadence de la science grecque.

Le travail et le système de Ptolémée reflètent tout à fait les qualités et malheureusement les défauts de la pensée scientifique grecque. En ayant l'idée d'un ordre permanent sous jacent du monde, les Grecs ainsi que Ptolémée ont créé la théorie scientifique et donné à la science le visage que nous lui connaissons aujourd'hui. Sous leur impulsion, l'astronomie s'est transformée en une science mathématique, fondée sur des observations précises et rigoureuses.

En demeurant toutefois encore trop abstraite, elle n'a pu réaliser la connexion entre mathématique et physique, entre calculs et expériences, qui conditionnent aujourd'hui le progrès des sciences quelles qu'elles soient, aussi la mathématique grecque annonce son déclin tout doucement mais l'école d'Alexandrie poursuit cependant  son effort. Mais la science grecque s'effondre dans des querelles mystiques de ses adeptes, et les derniers coups seront portés par les chrétiens hostiles à ce savoir, je cite, «païen». Les idées sombrent alors dans la confusion la plus totale. Rome à présent domine à son tour le monde, mais l'intérêt de ces derniers pour les mathématiques se limitera aux travaux d'arpentage.

L'apport des Grecs n'est pas pour autant perdu, rejeté par le monde chrétien, il va être sauvé par des moines qui recopient dès le 6^ème siècle après JC des manuscrits anciens et surtout par les astronomes du monde arabe qui vont recueillir l'héritage grec en même temps que celui des indiens.

L'Almageste était truffé d'anomalies mathématiques et astronomiques auxquelles Ptolémée ne prêtait aucune attention ou qu'il a dissimulé volontairement. Sa philosophie reposait sur le principe que si l'on croyait assez fort en une chose, on pouvait en ignorant le reste en démontrer l'existence : théorie assez étonnante…

Pour finir nous pourrons dire que Ptolémée fut probablement le plus génial compilateur de l'Antiquité. Il fut un très grand géographe mais en revanche il ne fut qu'un piètre astronome. Il fallut attendre plus de 1400 ans pour voir arriver Copernic et son système héliocentrique.

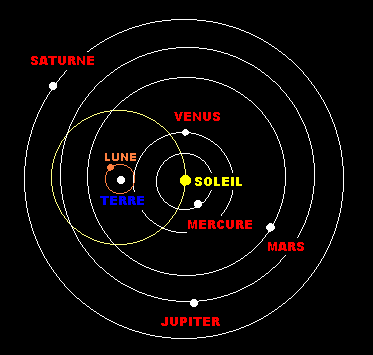
Le système héliocentrique

Equateur céleste et ecliptique

Retour haut page