Un peu d'histoire :
En 1671, l'astronome danois Olaus Römer fut invité à l'observatoire
d'Uraniborg, l'observatoire de Tycho Brahé sur l'île de Hven,
afin d'en déterminer la longitude de façon exacte. Pour calculer
celle-ci, Römer avait besoin d'une détermination extrêmement
précise de l'heure, destinée à mesurer le décalage horaire
entre le méridien d'origine et celui de Hven. La montre venait
tout juste d'être inventée par Huyghens, en 1657, et sa précision
laissait encore un peu à désirer.

Christian Huyghens essayant une nouvelle moumoute
Römer eût alors l'idée de se servir de la grande
horloge de la mécanique céleste en observant l'heure
des éclipses de Io, l'une des 4 principales lunes de Jupiter.
Pourquoi choisir Io ? La découverte du système jovien
en 1610 par Galilée avait considérablement frappé
les esprits et tout particulièrement la régularité
de métronome des éclipses et des occultations des
4 satellites galiléens. Une régularité qui
contrastait avec les imprécisions des montres de l'époque.
De plus, ces satellites présentaient un immense avantage
: tous les observateurs du même hémisphère terrestre
pouvaient contempler leurs éclipses simultanément,
indépendamment du lieu d'observation de chacun, ce qui facilitait
grandement la comparaison des observations et des mesures. De tous
les satellites galiléens, Io est celui dont l'orbite est
la plus proche d'un cercle parfait et, de surcroît, celui
dont la période orbitale est la plus courte : 1 jour 18 heures
28 minutes. Ces deux caractéristiques de Io garantissaient
donc des éclipses d'une très grande régularité
et d'une grande fréquence, ce qui facilitait l'accumulation
d'un grand nombre d'observations de qualité.

Olaus Römer dans sa cuisine en train de bricoler le tirage
de son barbecue
Au bout de 8 mois d'observations de ces éclipses, Römer
se rendit compte que quelque chose clochait : l'intervalle entre
chaque éclipse de Io variait très légèrement,
en fonction de la position de la Terre sur son orbite. Lorsque la
Terre était plus éloignée de Jupiter, les éclipses
avaient lieu plus tard que lorsque la Terre était au plus
près de Jupiter.
Au même moment, en 1668, Jean-Dominique Cassini, l'astronome
de Louis XIV, mettait au point les premières tables de prévision
des éclipses et des occultations des satellites galiléens.
Pour affiner ses calculs, Cassini fit venir en 1672 Olaus Römer
à l'observatoire de Paris-Meudon et lui confia la mission
de comparer systématiquement les observations des satellites
de Jupiter et ses propres tables.

J-D Cassini en train de ramener sa fraise
Très vite, les deux astronomes se rendirent compte que lorsque
la Terre et Jupiter étaient en opposition, les éclipses
commençaient en avance alors qu'au moment de la conjonction,
elles se produisaient en retard. Les observations et les tables
de Cassini ne coïncidaient réellement qu'au moment où
Jupiter et la Terre étaient en quadrature
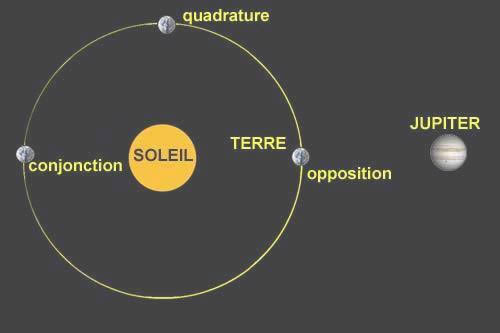
Schéma ASCT-astronomie / Ph Ledoux
Olaus Römer trouva assez rapidement la solution de cette
énigme : la lumière de Io ne se déplace pas instantanément
dans l'espace, comme on le croyait autrefois. Au contraire,
elle a besoin de quelques minutes pour nous parvenir. Et plus
Io est éloignée de la Terre, plus sa lumière met de temps
à nous atteindre. En septembre 1676, Römer publia sa découverte
dans le Journal des Sçavans et prédit que la prochaine
éclipse de Io, prévue pour le 9 novembre, aurait lieu avec
10 mn de retard sur l'heure prévue. Sensation ! La prédiction
s'avéra juste ! Sur ces bases, les collaborateurs de Römer
estimèrent que la lumière se déplaçait de Io vers la Terre
à la vitesse de 214 000 km/s. Mais ses détracteurs ne désarmèrent
pas pour autant, notamment l'astronome Jean-Dominique Cassini
qui continua d'affirmer longtemps que les irrégularités des
éclipses de Io étaient dûes à des anomalies dans la force
d'attraction gravitationnelle de Jupiter sur Io. Il fallut
attendre les travaux de James Bradley, en 1729, et de Jean-Baptiste
Delambre en 1809 pour que la thèse de Römer l'emporte enfin.
Calculez vous-même la vitesse
de la lumière :
Mettons-nous au boulot, exactement comme le fit Römer. Tout
d'abord, entendons-nous bien sur quelques définitions :
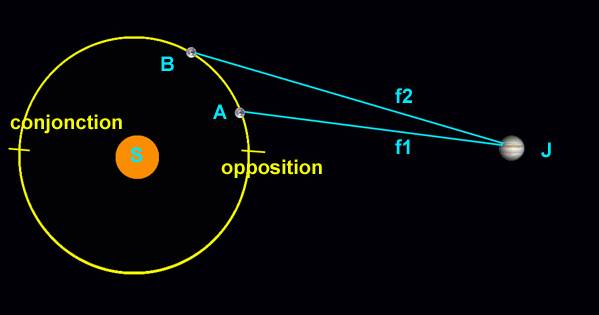
Schéma ASCT-astronomie / Ph Ledoux
S = la position du Soleil
J = la position de Jupiter et de Io
A = la position de la Terre sur son orbite au moment de la première
éclipse de Io
B = la position de la Terre sur son orbite au moment de l'éclipse
suivante de Io
f1 = la distance entre la Terre et Jupiter le (AJ = f1)
f2 = la distance entre la Terre et Jupiter le (BJ = f2)
c = la vitesse de la lumière
T = la période de révolution de Io sur son orbite
autour de Jupiter. T = 1 jour 18 heures 28 minutes = 1,769 jour
t = l'intervalle de temps qui sépare, pour l'observateur
terrestre, 2 éclipses de Io dans le cône d'ombre de
Jupiter
Durant cet intervalle t, la Terre s'est déplacée sur son
orbite autour du Soleil, passant de la position A à la position
B et, ce faisant, s'est un peu éloignée de Jupiter et Io
Si la lumière se déplaçait instantanément dans l'espace,
la deuxième éclipse de Io surviendrait au bout d'une révolution
complète de Io autour de Jupiter, c'est à dire au bout de
l'intervalle de temps T = 1,769 jour. Les données chiffrées
ci-dessous montrent bien que ce n'est pas le cas : la deuxième
éclipse survient au bout d'une durée de t, laquelle n'a pas
la même valeur que T. En fait, comme la vitesse de la lumière
n'est pas infinie mais limitée, il s'écoule une durée de t
+ T entre deux éclipses de Io par Jupiter
Début des éclipses de Io entre le passage de Jupiter
en conjonction, le 17 novembre 1994, 20 H, et son passage en opposition
le 1er juin 1995, 11 H.
00 14/12/94 08h37 34 12/02/95 12h41 68 13/04/95 16h41
01 16/12/94 03h06 35 14/02/95 07h09 69 15/04/95 11h09
02 17/12/96 21h34 36 16/02/95 01h37 70 17/04/95 05h37
03 19/12/94 16h03 37 17/02/95 20h05 71 19/04/95 00h05
04 21/12/94 10h31 38 19/02/95 14h34 72 20/04/95 18h34
05 23/12/94 04h59 39 21/02/95 09h02 73 22/04/95 13h02
06 24/12/94 23h28 40 23/02/95 03h30 74 24/04/96 07h30
07 26/12/94 17h56 41 24/02/95 21h58 75 26/04/95 01h59
08 28/12/94 12h25 42 26/02/95 16h27 76 27/04/95 20h27
09 30/12/94 06h53 43 28/02/95 10h55 77 29/04/95 14h55
10 01/01/95 01h21 44 02/03/95 05h23 78 01/05/95 09h23
11 02/01/95 19h50 45 03/03/95 23h51 79 03/05/95 03h52
12 04/01/95 14h18 46 05/03/95 18h19 80 04/05/95 22h20
13 06/01/95 08h46 47 07/03/95 12h48 81 06/05/95 16h48
14 08/01/95 03h15 48 09/03/95 07h16 82 08/05/95 11h17
15 09/01/95 21h43 49 11/03/95 01h44 83 10/05/95 05h45
16 11/01/95 16h11 50 12/03/95 20h12 84 12/05/95 00h14
17 13/01/95 10h40 51 14/03/95 14h41 85 13/05/95 18h42
18 15/01/95 05h08 52 16/03/95 09h09 86 15/05/95 13h10
19 16/01/95 23h36 53 18/03/95 03h37 87 17/05/95 07h39
20 18/01/96 18h05 54 19/03/95 22h05 88 19/05/95 02h07
21 20/01/95 12h33 55 21/03/95 16h33 89 19/05/95 20h36
22 22/01/95 07h01 56 23/03/95 11h02 90 22/05/95 15h04
23 24/01/95 01h30 57 25/03/95 05h30 91 24/05/95 09h32
24 25/01/95 19h56 58 26/03/95 23h58 92 26/05/95 04h01
25 27/01/95 14h26 59 28/03/95 18h26 93 27/05/95 22h29
26 29/01/95 08h55 60 30/03/95 12h55 94 29/05/95 16h58
27 31/01/95 03h23 61 01/04/95 07h23 95 31/05/95 11h26
28 01/02/95 21h51 62 03/04/95 01h51
29 03/02/95 16h19 63 04/04/95 20h19
30 05/02/95 10h48 64 06/04/95 14h48
31 07/02/95 05h16 65 08/04/95 09h16
32 08/02/95 23h44 66 10/04/95 03h44
33 10/02/95 18h12 67 11/04/95 22h12
Lorsque la Terre est au point A, l'observateur terrestre voit la
deuxième éclipse au bout d'une durée t + f1
/ c
Et lorsque la Terre est arrivée en B, il la voit au bout
d'une durée t + T + f2 / c
La différence de temps entre deux éclipses consécutives
de Io est alors égale à [t + T + f2 / c] - [t + f1
/ c] = T + (f2 - f1) / c
L'équation pour trouver la vitesse de la lumière
devient alors très facile à résoudre : il suffit
de diviser la différence de temps entre deux éclipses
successives de Io par T + f2 - f1
Tentez le coup avec deux éclipses successives de Io dans
le tableau ci-dessus et vous verrez que çà marche
...
Les imprécisions de la méthode de Römer :
La méthode de Römer présente néanmoins
plusieurs imperfections, sources d'erreurs :
--- la limite du limbe de Jupiter n'est pas nette, en raison
de l'épaisse atmosphère de Jupiter qui diffuse la lumière
: la disparition de Io dans le cône d'ombre de Jupiter ne
s'effectue donc pas instantanément mais progressivement, ce
qui interdit toute mesure vraiment précise de l'instant exact
de l'éclipse.
--- d'autre part, Io n'est pas un point mais un petit disque
doté d'un certain diamètre apparent : là encore, de ce fait,
sa disparition dans l'ombre de Jupiter ne s'effectue pas instantanément.
--- autre difficulté : l'éclipse de Io ne se produit pas
toujours au niveau de l'équateur de Jupiter et par conséquent,
le diamètre de l'ombre de Jupiter n'est pas toujours identique
d'une éclipse à l'autre. La traversée du cône d'ombre de Jupiter
par Io peut donc prendre un temps variable.
--- au moment de la conjonction, Jupiter est dans l'alignement
du Soleil pour les astronomes terrestres, ce qui rend toute
observation impossible à ce moment-là : observer Jupiter dans
ces conditions équivaudrait à se brûler la rétine de
l'oeil avec la lumière du Soleil concentrée par le télescope.

Schéma ASCT-astronomie / Ph Ledoux
Au moment de l'opposition, nouveau pépin : l'ombre de Jupiter
est totalement cachée par ce dernier et les éclipses deviennent
invisibles. Il faut donc à ce moment-là se contenter d'observer
les occultations de Io par le disque jovien. Mais avant et après l'opposition, les choses ne sont pas
pour autant plus simples : avant l'opposition (position A),
si l'observateur terrestre voit parfaitement le début de chaque
éclipse de Io, par contre leur fin lui est cachée par le disque
de Jupiter. Après l'opposition (position B), difficulté inverse
: Jupiter fait écran entre la Terre et le début de chaque
éclipse de Io. Par contre, la fin de l'éclipse est alors devenue
parfaitement observable
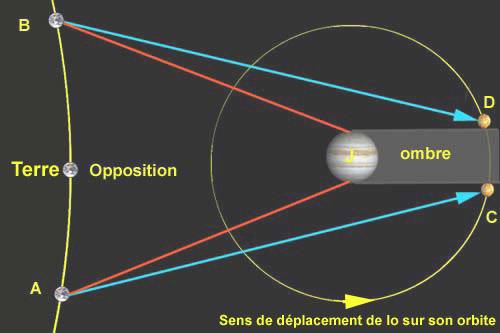
Schéma ASCT-astronomie / Ph Ledoux
Bref, devenir un petit génie de l'astronomie n'est vraiment
pas une chose si facile ...

Merci Greg !
|