INTRODUCTION :
C'est dans le propre des hommes de tout classer, ranger pour pouvoir
comparer, retrouver facilement ce qui aura été répertorié. Ainsi,
tout objet observable dans le ciel est forcément repérable
dans un système de coordonnées. Comme sur la Terre, l'homme a besoin
d'un système de repérage afin de localiser un astre.
Pour tout système de ce type il est nécessaire d'avoir un point
d'origine, un point zéro. Ce dernier est arbitraire et l'homme
va pouvoir jouer sur cet élément pour définir des systèmes
différents de coordonnées.
LES COORDONNEES TERRESTRES :
|
|
Ce système de coordonnées a pour plan principal
l'équateur terrestre et la ligne des pôles lui est perpendiculaire.
On a choisi comme méridien d'origine le méridien qui passe
par l'observatoire de Greenwich.
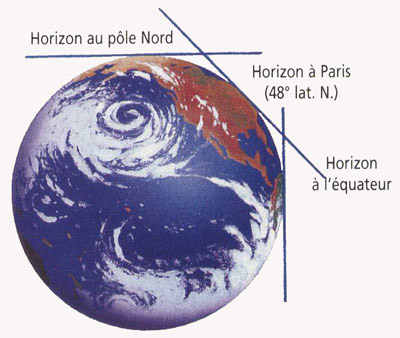
La latitude d'un lieu A sera sa distance angulaire à l'équateur
; elle est égale à la hauteur du pôle au-dessus de l'horizon.
La longitude est l'angle que fait le méridien local avec
celui de Greenwich G.
|
Mais en fonction des astres que nous voulons observer, certains
systèmes de coordonnées sont plus ou moins pratiques à utiliser
pour un astronome amateur. Il existe principalement 4 types de coordonnées
utilisés en astronomie :
1 ) Le système de coordonnées horizontales ou
azimutales
2 ) Le système de coordonnées équatoriales
3 ) Le système de coordonnées écliptiques
4 ) Le système de coordonnées galactiques
auxquels il faut rajouter un système hybride, très
employé par les marins : le système de coordonnées
horaires.
LES COORDONNEES AZIMUTALES :
C'est le système de coordonnées le plus simple à utiliser, mais
pas forcément le plus utile. Dans le cas de ces coordonnées,
l'observateur est défini comme étant le point d'origine de
tout le système. On projette autour de lui une sphère imaginaire
sur laquelle toutes les étoiles viennent se coller. Cette sphère
imaginaire est appelée sphère céleste locale.
L'horizon est représenté par le plan de l'horizon, l'observateur
voit donc tout ce qui est au dessus de ce cercle. S'il regarde directement
à la verticale au-dessus de lui, le point le plus haut est
appelé le zénith (l'opposé de ce point est le nadir,
mais il ne le voit pas puisqu'il est situé sous ses pieds).
On peut noter que pour un observateur diamétralement opposé à lui
sur la Terre, son zénith correspond au nadir du dit observateur.
Nous utiliserons le plan de l'horizon comme plan de référence
et nous définirons 2 coordonnées à partir de
ce plan : l'AZIMUT et la HAUTEUR.
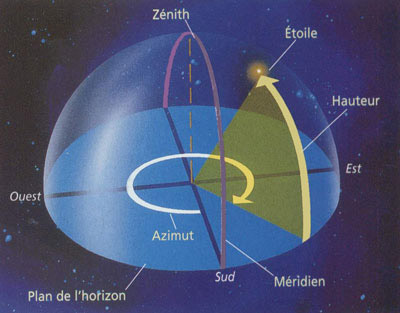
La coordonnée en azimut :
Le point d'origine des azimuts a été fixé, en astronomie,
au SUD, puis compté de 0° à 360° dans le sens des aiguilles
d'une montre. De ce fait, nous allons trouver plein Sud, le 0°,
puis à l'Ouest 90°, puis au Nord l'azimut 180° ensuite
à l'Est l'azimut 270° puis enfin nous revenons au Sud avec l'azimut
360° ou 0°.
Petite remarque : les marins emploient ce type de coordonnées,
mais ils ont décidé de fixer l'origine des azimuts
au Nord, et ils comptent dans le même sens.
La coordonnée en altitude ( h ) :
Le point d'origine des hauteurs a été fixée sur l'horizon, puis
comptée de 0° à 90° en partant de l'horizon vers le zénith.
Donc nous avons 0° à l'horizon, et 90° au dessus de notre tête (
au zénith ).
Les deux axes de coordonnées étant ainsi définis,
nous pouvons donc maintenant localiser aisément une étoile,
grâce à sa coordonnée en azimut et à
sa coordonnée en altitude.
Il existe dans ce système une coordonnée complémentaire
: la distance zénithale. C'est l'angle que font le zénith et l'étoile
visée. En fait hauteur de l'astre + distance zénithale du
même astre = 90 °. Remarque : le cercle (non représenté ici) passant
par l'étoile et parallèle à l'horizon est l'almancatara,
c'est un parallèle de hauteur. L'analogie avec les coordonnées
terrestres donne :
équateur = horizon
pôle = zénith
latitude = hauteur
méridien = azimut
Du fait que l'observateur représente le centre du système, nous
nous rendons vite compte qu'une coordonnée fournie dans ce référentiel,
n'est valable que pour un lieu donné et pour un instant précis ce
qui n'est pas très exploitable en astronomie : les coordonnées
d'une étoile ne seront pas les mêmes selon que vous
l'observerez du Havre ou bien de Brest. Sans compter que la rotation
de notre bonne vieille planète, qui entraîne dans son mouvement
tous les objets dans le ciel, va sans cesse modifier les coordonnées
de l'étoile !
Bref : les coordonnées horizontales/ azimutales d'un astre varient
continuellement ... pas facile pour communiquer entre astronomes
...
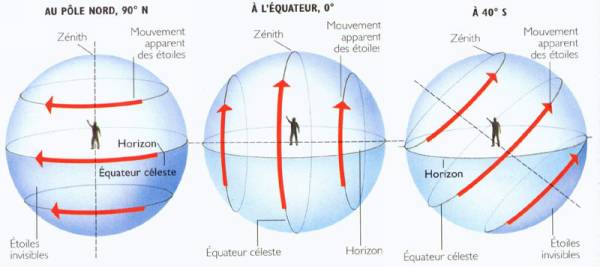
LES COORDONNEES EQUATORIALES :
C'est le système de coordonnées le plus utilisé en astronomie.
Quand vous devez spécifier un point à la surface de la Terre, vous
utilisez ce que les géomètres appellent les coordonnées sphériques,
ce que nous appelons usuellement " LATITUDES & LONGITUDES "
Imaginons maintenant que nous projetions ces latitudes et ces longitudes
sur la sphère céleste, nous obtenons alors respectivement les DECLINAISONS,
et les ASCENSIONS DROITES.
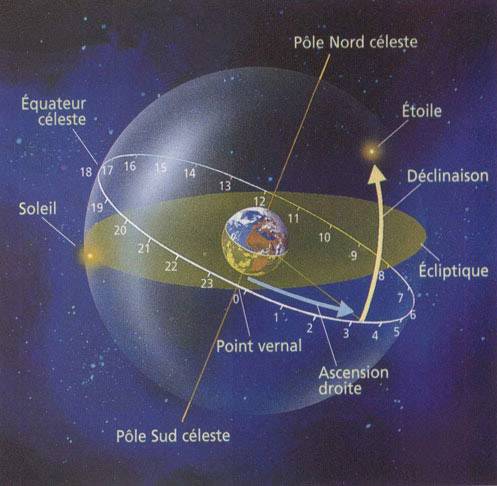
Il y a énormément de choses à dire sur ce type de coordonnées.
Fonctionnement : nous avons vu que le système azimutal dépendait
du lieu de l'observateur. Dans le système équatorial,
le point d'origine est différent : c'est le centre de la
Terre. De même, le plan de référence ne sera plus l'horizon
mais l'équateur céleste. Ce dernier est la projection de l'équateur
terrestre dans l'espace.
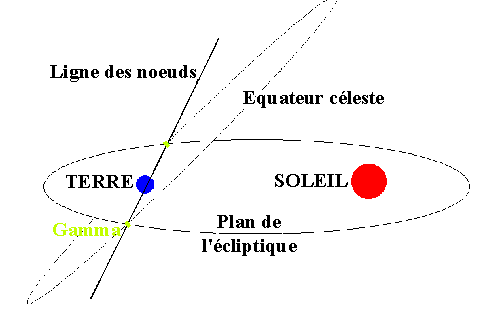
a) Le point vernal :
Les planètes tournent autour du Soleil dans un plan appelé l'écliptique.
|
|
|
le système solaire et le plan de l'écliptique
vus de profil
|
|
|
le système solaire et le plan de l'écliptique
vus de 3/4
|
Ainsi le Soleil décrit dans le ciel, en un an, un mouvement apparent
vu depuis la Terre comme un grand cercle : ce cercle, c'est l'écliptique.
L'intersection de l'équateur céleste et de l'écliptique donne une
droite appelée ligne des nouds. Les deux plans se coupent en deux
points (deux noeuds) et l'angle formé par ces deux plans est de
23°27' : c'est l'obliquité de l'écliptique. L'un de ces points est
appelé le POINT VERNAL (ou point gamma) : il
correspond au noud ascendant. C'est le point de référence de notre
système, il se trouve dans le plan de l'équateur céleste. Toutes
les ascensions droites seront comptées à partir de
ce point zéro.
b) Remarque :
Durant l'année, le soleil passera donc au-dessus de l'équateur
céleste (déclinaison positive) entre le printemps et l'automne,
puis en-dessous (déclinaison négative) de l'équateur céleste entre
l'automne et le printemps suivant. Ainsi le Soleil coupe dans sa
course montante l'équateur céleste au niveau du noud ascendant au
moment de l'équinoxe du printemps. Puis il coupe l'équateur céleste
dans sa course descendante au niveau du noud descendant au moment
de l'équinoxe d'automne.
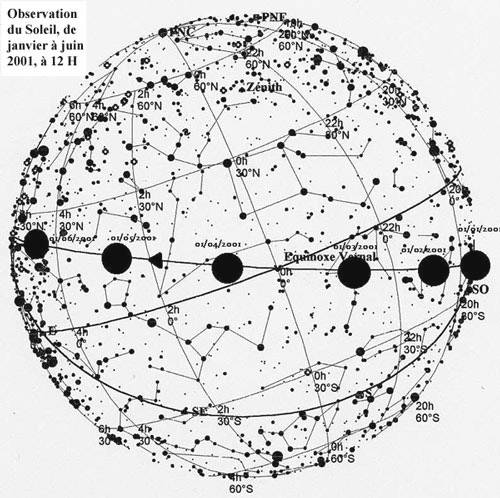
Les points intermédiaires sont les solstices. Le mot équinoxe veut
dire égalité entre la durée de la nuit et du jour. Le mot solstice
signifie immobilité (apparente) du Soleil dans le ciel.
Mais revenons à la définition de la déclinaison
et de l'ascension droite :
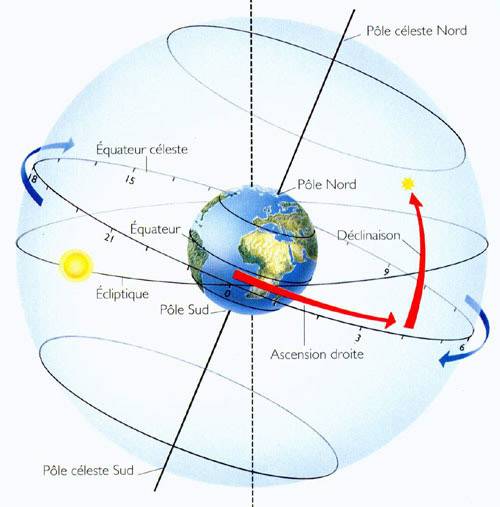
c) La DECLINAISON ( souvent symbolisée par la lettre grecque
Delta ) :
Les déclinaisons sont arbitrairement comptées positivement de l'équateur
vers le pôle Nord, et négativement de l'équateur vers le pôle Sud.
Le pôle Nord se trouvant à + 90°, l'équateur matérialise l'origine
des déclinaisons donc 0°, le pôle Sud, se trouvant lui à - 90° de
déclinaison.
Notez que l'équateur dans le ciel se trouve toujours à une hauteur
de 90° - la latitude du lieu d'observation. Par exemple, pour Le
Havre, l'équateur céleste dans la direction du Sud sera à
une hauteur de 90° - 49°31' soit 40°29'.
d) L'ASCENSION DROITE (souvent symbolisée par la lettre
grecque Alpha) :
Le point d'origine des coordonnées d'ascensions droites
est le point vernal (point gamma ). L'ascension droite se mesure
en sens opposé à celui de la rotation diurne de la sphère céleste
(donc comptée positivement vers l'Est à partir du
point vernal). Elle peut être chiffrée en degrés d'angle de 0° à
360°, mais les astronomes ont coutume de l'exprimer en heures, minutes
et secondes, ce qui est finalement assez logique puisqu'il faut
24 H pour que la rotation de la Terre nous fasse parcourir ce grand
cercle.

Avec ce système de coordonnées équatoriales,
la position d'une étoile est définie une bonne fois
pour toutes grâce à sa déclinaison et à
son ascension droite et celà pour tous les observateurs terrestres
et quelque soit la saison d'observation.
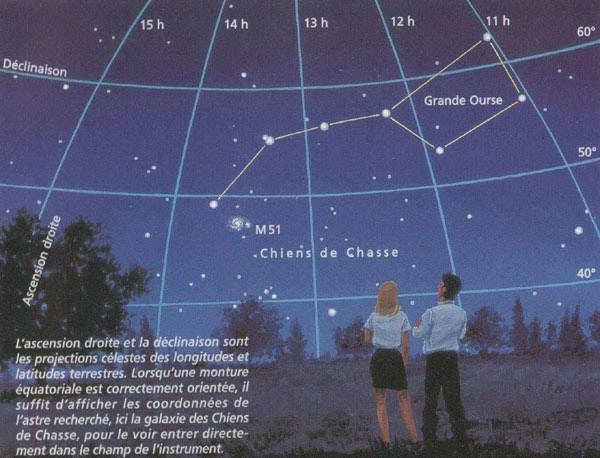
Mais pour un observateur sur la Terre il n'y a rien de fixe dans
ce dispositif de coordonnées, mais au contraire une espèce de manège
infernal où le Soleil et le système de coordonnées tourne
par rapport à lui. C'est pourquoi le système de coordonnées
équatoriales n'est utilisé que par les astronomes
: une fois leur télescope soigneusement mis en station, avec
l'axe d'ascension droite bien calé en direction du pôle
Nord céleste, il leur suffit de se servir des graduations
de l'axe d'ascension droite et de l'axe de déclinaison pour
pointer des nébuleuses ou des galaxies invisibles à
l'oeil nu : elles seront alors pile dans le champ de l'oculaire
du télescope.

e) Les choses se compliquent ...
Malheureusement, ce système de coordonnées si apprécié
des astronomes n'est pas d'une fiabilité totale : en effet
la Terre, sous l'influence du Soleil, de la Lune et des autres planètes,
voit son axe de rotation perturbé : celui-ci se déplace et
effectue un tour complet en 26 000 ans, à la manière
d'une toupie. C'est ce que les astronomes appellent le phénomène
de précession.
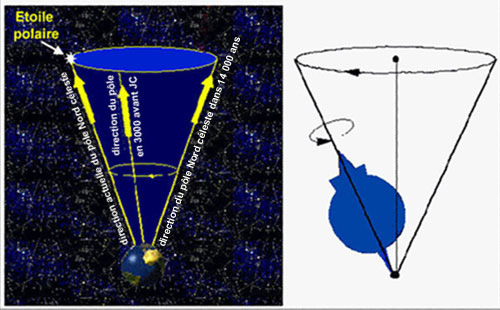
Ainsi notre étoile polaire actuelle ne montrera le pôle
Nord dans l'avenir. Dans 11000 ans, c'est l'étoile Véga
de la Lyre qui sera la plus proche du pôle Nord céleste. Il
y a 3000 ans c'était Tubhe, la principale étoile de la
constellation du Dragon.
En plus de ce mouvement de précession, il existe une deuxième
perturbation, sous la forme d'une oscillation périodique de faible
amplitude : c'est la nutation.
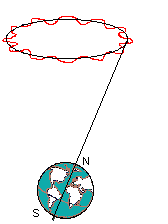
Ces mouvements de l'axe de rotation de la Terre sont dus aux actions
cumulés du soleil, de la lune et des planètes du système
solaire. Il faut encore y ajouter le mouvement propre des étoiles
: chacune d'entre elle vit sa vie et se déplace au sein de
notre galaxie au fil des grands courants d'étoiles qui l'agite.
De ce fait, au cours des millénaires, la position des étoiles
varie.
La précession, la nutation et le mouvement propre des étoiles affectent
donc nos belles coordonnées célestes équatoriales, ce qui
oblige les astronomes à les corriger dans le temps, et donc
de spécifier l'EPOQUE pour laquelle elles sont fournies.
Par convention, l'époque change tous les 50 ans. Nous pouvons donc
utiliser encore actuellement les coordonnées J2000 sans introduire
trop d'erreurs dans nos pointages d'étoiles.
f) Quelques équations pour les forts en maths :
Pour convertir les coordonnées équatoriales en coordonnées
azimutales, il existe deux équations :
L'équation (1) permet de calculer la hauteur. Quand on remplace
l'équation (3) dans l'équation (2), on trouve, en
simplifiant, la formule permettant de calculer l'azimut :
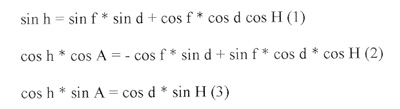
Bien évidemment, il existe également des équations
permettant de convertir des coordonnées altazimutales en
coordonnées équatoriales :
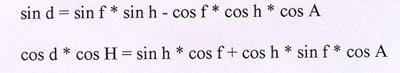
g) Quelques autres définitions :
|
|
Le demi-cercle PN, zénith, Sud, PS est appelé méridien local.
Quand un astre se trouve au méridien local, on dit aussi qu'il
culmine ou qu'il transite. C'est à ce moment
que l'astre est au plus haut dans le ciel. Les autres demi
cercles sont appelés cercles horaires. La sphère céleste accomplit
en effet presque exactement un tour complet en un jour sidéral,
lequel est divisé en 24 H comme le jour solaire. C'est pour
cette raison que l'on peut donc dire que les 360° sont parcourus
en 24 H. En 1 heure une étoile parcourt 15° dans le
ciel ( 360 / 24 =15 ). Dans le prolongement de ce raisonnement,
en 1 minute de temps, une étoile parcourt 15' d'arc,
et en 1 seconde de temps, 15" d'arc.Tandis que hauteur et
azimut d'un astre varient continuellement, la déclinaison
et l'ascension droite demeurent, l'une et l'autre, inchangées.
En effet, durant la rotation de la sphère céleste, la distance
d'un astre à l'équateur ne varie pas, ainsi que l'angle (
a ) = point vernal ( g ) - méridien de l'étoile, puisque le
point vernal est lui aussi entraîné dans la rotation apparente
de la sphère céleste. De plus ce type de coordonnées n'est
pas lié au lieu d'observation. Le système de coordonnées équatoriales
décrit précédemment est donc très pratique pour définir des
positions d'objets célestes dans l'absolu mais ce système
de coordonnées tourne est entraîné dans
le ciel par la rotation de la Terre. Les astronomes ont donc
défini deux autres systèmes de coordonnées pour essayer de
se faciliter la vie. Cette apparente complexité cache en fait
une habile combinaison entre les dispositifs d'observations,
de mesure, et de calcul. Ces deux systèmes sont de type coordonnées
sphériques et portent les noms de :
. Coordonnées azimutales, déjà décrites
plus haut
. Coordonnées horaires
|
|
h) Un petit exercice pratique sympa à réaliser :
repérer Jupiter en plein jour :
Ce petit exercice d'observation est facile à réussir
au moyen d'une simple paire de jumelles montées sur un trépied
photographique. Il suffit de connaître, grâce aux éphémérides,
l'heure du passage de Jupiter au méridien de votre lieu d'observation.
Les astronomes appellent également cet instant le "transit"
de Jupiter devant cette ligne imaginaire qui va du pôle Nord
au pôle Sud en passant par votre jardin. Vous verrez également
parfois employé le terme de "culmination" de Jupiter
puisque le franchissement du méridien correspond au moment
où Jupiter sera le plus haut dans le ciel.
Commencez par installer vos jumelles et leur trépied sur
la ligne imaginaire de votre méridien, en direction du Sud,
et réglez leur inclinaison par rapport à la ligne
d'horizon pile poil sur la hauteur qu'aura Jupiter au moment de
son transit : les éphémérides vous indiquent
la déclinaison de Jupiter dans le ciel. Vous n'avez plus
alors qu'à effectuer une petite conversion grâce à
l'équation ci-dessous :
hauteur de Jupiter au-dessus de l'horizon = 90° - la latitude
votre lieu d'observation + la déclinaison de Jupiter.
Si vous ignorez votre latitude, vous trouverez ci-joint un
tableau indiquant la latitude
des principales villes de France. Vous trouverez également,
sur Internet, un petit site qui recense les coordonnées
géographiques de pratiquement tous
les patelins de France.
Eventuellement, pour bien régler la hauteur de vos jumelles,
aidez-vous d'un rapporteur.

Plus sophistiqué, le théodolite atomique à
rétropédalage exponentiel et molette pithécanthropique
du club d'astronomie de Toussaint :

Ensuite, il ne vous reste plus qu'à attendre l'heure du
passage de Jupiter au méridien donnée par les éphémérides
: à cet instant précis, le petit dique blanc de Jupiter
sera en plein dans le champ de vos jumelles.
Si vous souhaitez une plus grande précision, pensez à
corriger l'heure des éphémérides, qui est donnée
généralement pour le méridien de Greenwich
(0° de longitude), en fonction la longitude de votre lieu d'observation
: c'est très facile, il vous suffit d'enlever 4 minutes pour
chaque degré de longitude de différence avec Greenwich
si vous habitez à l'Est de son méridien et, au contraire,
d'ajouter 4 minutes pour chaque degré de longitude si vous
habitez plus à l'Ouest. Petit exemple pratique : Fécamp
est situé à 0 degré 25 mn d'arc à l'Est
du méridien de Greenwich, soit, "grosso modo",
un demi-degré de différence. Il faut donc corriger
l'heure donnée par les éphémérides en
y apportant une correction de - 2 minutes. Attention cependant :
parfois, certaines éphémérides sont données
non pas pour le méridien de Greenwich mais pour celui de
Paris, qui est situé par 2 degrés 20 mn de longitude
Est. Le principe de correction à appliquer reste cependant
analogue. Pour vous fixer les idées, vous trouverez ci-joint
un tableau qui vous fournira la correction
horaire en fonction de la longitude des principales villes de France.
LES COORDONNEES HORAIRES :
Ce système est un hybride entre le système azimutal et
le système équatorial. On utilise ici aussi le pôle
céleste et l'équateur céleste. Le plan de
référence sera l'équateur céleste et le point d'origine le sud
(méridien local). Ce système est très employé
par les marins.
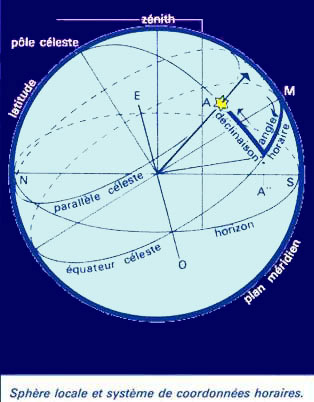
a) L'angle horaire ( H) :
L'angle horaire est l'angle dièdre entre le méridien
du lieu et le cercle horaire de l'astre. L'étoile est toujours
sur le même "parallèle" (déclinaison)
mais son "méridien" varie avec l'heure et le
lieu. Dans ce cas là, seul l'angle horaire variera (quand une
heure passe, l'angle horaire H augmente d'une heure) il est compté
positivement dans le sens rétrograde, en heures et ses fractions.
Sur le schéma il est représenté par l'angle H.
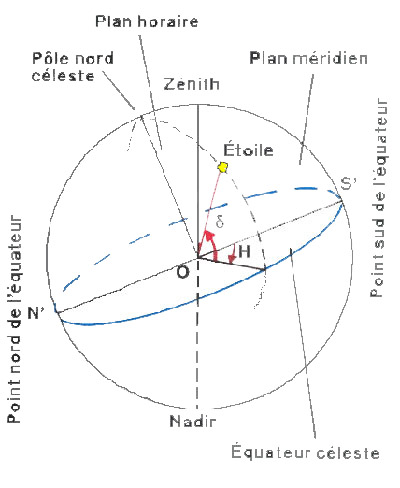
L'angle horaire du point vernal (gamma) appelé T varie donc aussi
au cours du temps. Il est appelé le TEMPS SIDERAL mais
c'est un angle.
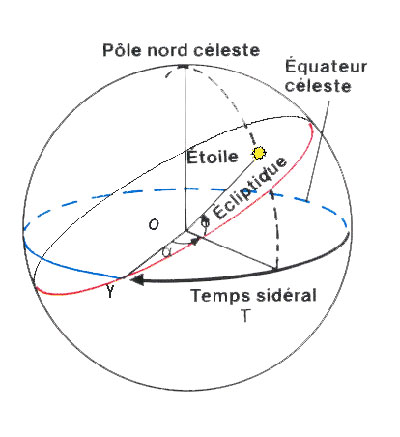
c) La déclinaison (d) :
La déclinaison dans le système horaire reste inchangée
par rapport au système équatorial des astronomes.
LES COORDONNEES ECLIPTIQUES :
Beaucoup moins utilisé pour le positionnement des objets du ciel
profond, ce système de coordonnées est surtout employé pour définir
l'emplacement des objets du système solaire. Etant donné que la
plupart des objets gravitant dans le système solaire sont regroupés
quasiment dans le même plan ( sauf Pluton, quelques astéroïdes,
et les comètes ), il a été défini un nouveau référentiel : le
centre du système n'est plus le centre de la Terre mais
le centre du Soleil et le plan de référence n'est
plus l'équateur céleste mais l'écliptique,
c'est à dire le plan de révolution de la Terre autour du
Soleil.
L'origine de ce référentiel est encore une fois notre fameux
point vernal.
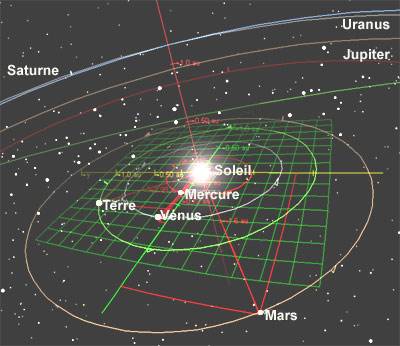
les axes et le "quadrillage" des coordonnées
écliptiques
Fonctionnement :
a) La longitude écliptique ( l ) :
La longitude écliptique est comptée sur l'écliptique de 0 à 360
° dans le sens direct, l'origine étant le point vernal. On l'emploie
parfois pour les observations comparatives portant sur de longues
périodes, car ce type de coordonnées est plus stable, du fait
que le plan de l'écliptique reste bien plus stable que le plan
équatorial. On néglige bien souvent la nutation.
b) La latitude écliptique ( b ) :
La latitude céleste est comptée positivement de 0 à 90° entre
l'écliptique et le pôle Nord écliptique, et négativement dans
l'autre sens.
LES COORDONNEES GALACTIQUES :
Dans les coordonnées galactiques géocentriques, l'angle est compté
à partir du centre de la galaxie sur le plan galactique. Ce système
de coordonnées n'est employé que pour l'étude de
notre galaxie et le repérage des objets extragalactiques. Je n'ai
pas encore vu d'applications en astronomie amateur. Les coordonnées
galactiques sont la latitude et la longitude galactique(s)
|